Assertion : The rms velocity and most probable speeds of the molecules in a gas are same.
The Maxwell distribution curve for the speed of the molecules in a gas is symmetrical.

A

If both assertion and reason are true and reason is the correct explanation os assertion.

B

If both assertion and reason are true but reason is not be correct explanation of assertion.

C

If assertion is true but reason is false.

D

If both assertion and reason are false.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

$v_{r m s} = \sqrt{\frac{3 k_{B} T}{m}} or, \sqrt{\frac{3 R T}{M}}$
$v_{probable} = \sqrt{\frac{2 k_{B} T}{m}} or, \sqrt{\frac{2 R T}{M}}$
Maxwell distribution of speed is as shown

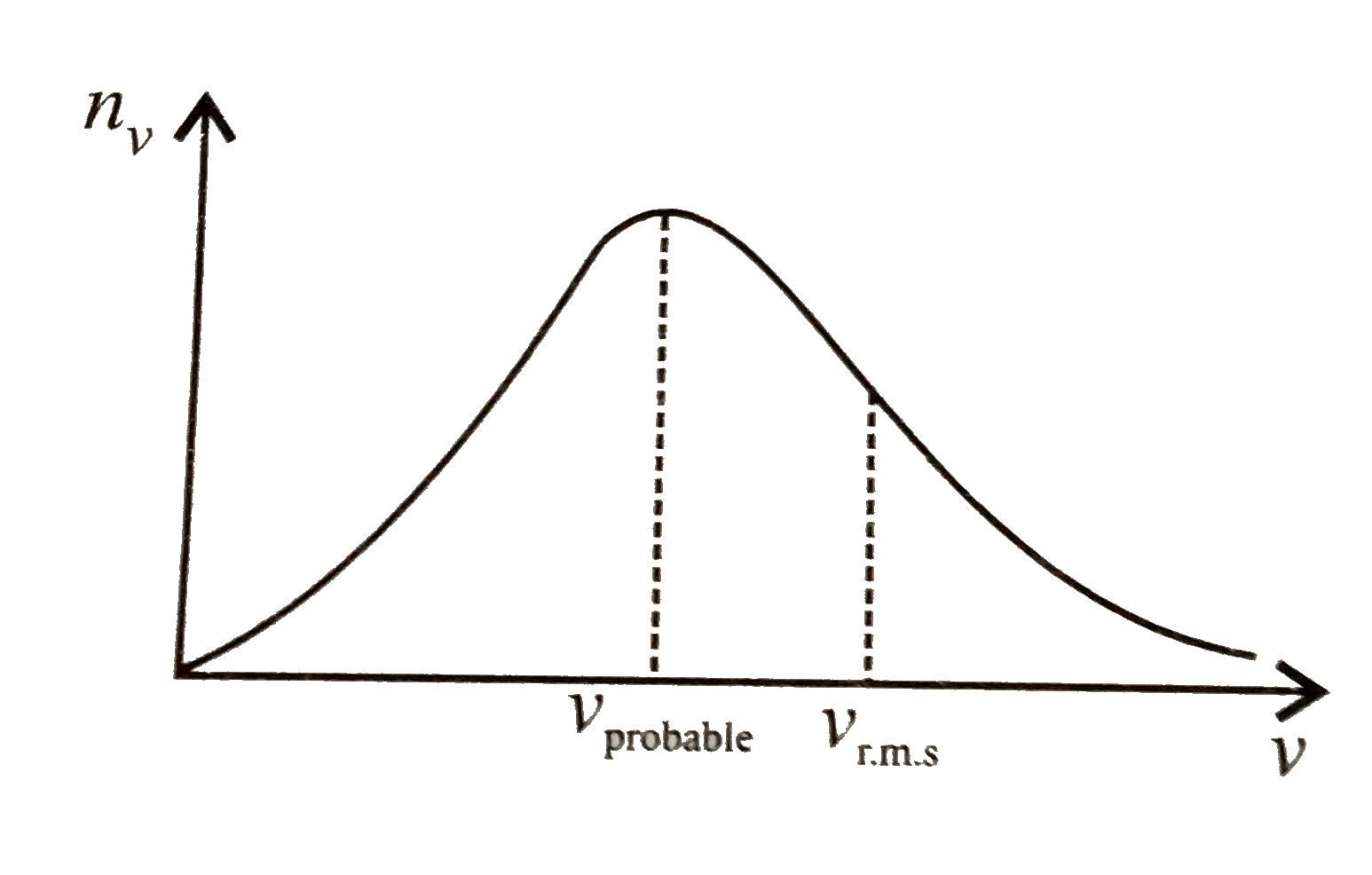
This is asymmetic. Therefore reason is also wrong.

|

Updated on:21/07/2023

Class 11 PHYSICS KINETIC THEORY OF GASES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Assertion : The root mean sguar and most probable speed of the molecules in a gas are the same
Reason : The Maxwell distribation for the speed of molecules in a gas is symentrical
AIf both assertion and reason are true and the reason is the correct explanation of assertion.
BIf both assertion and reason are true but reason is not the correct explanation of assertion.
CIf assertion is true statement but reason is false.
DIf both assertion and reason are false.
Question 2 - Select One
The rms speed of a gas molecule is
A $\sqrt{\frac{M}{3 R T}}$
B $\frac{M}{3 R T}$
C $\sqrt{\frac{3 R T}{M}}$
D ${(\frac{3 R T}{M})}^{2}$
Question 3 - Select One
$v_{r m s}, v_{a v}$ and $v_{m p}$ are root mean square average and most probable speeds of molecules of a gas obeying Maxwellian velocity distribution. Which of the following statements is correct ?
A $v_{r m s} < v_{a v} < v_{m p}$
B $v_{r m s} > v_{a v} > v_{m p}$
C $v_{m p} < v_{r m s} < v_{a v}$
D $v_{m p} > v_{r m s} > v_{a v}$

NCERT FINGERTIPS-KINETIC THEORY-Assertion And Reason

Home
Ask Doubt
Profile