In the question number of 45, the equivalent thermal conductivity of the compound bar is
K1K2K1+K2
2K1K2K1+K2
K1K1+K2
K2K1+K2
The correct Answer is:B
Let K be thermal conductivity of the temperature bar.
Heat current through the compound bar of length 2L is H=KA(T1−T2)2L
At steady state, H=H1=H2
∴KA(T1−T2)2L=K1A(T1−T0)L…...(ii)
Substituting the value of T0 Eq (i) in (ii), we get
K(T1−T2)2=K1[T1−(K1T1+K2T2(K1+K2))]=K1K2(T1−T2)(K1+K2)
⇒=2K1K2K1+K2
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Newton'S Law Of Cooling
3 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Higher Order Thinking Skills
8 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTIPSCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Change Of State
13 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSBOOK - NCERT FINGERTIPSCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONSEXERCISE - Assertion And Reason
15 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTIPSCHAPTER - THERMODYNAMICSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Thermal conduction
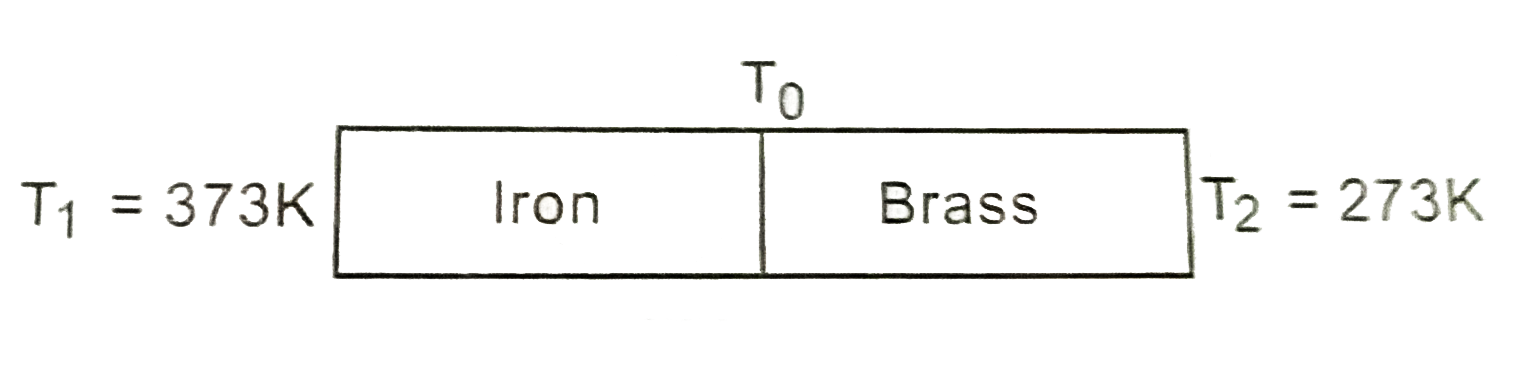
View SolutionAn iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
 .
.
View Solution
Knowledge Check
The unit of thermal conductivity is :
AWm−1K−1BJm−1K−1CJm−1K−1DWmK−1Two rods of length l and 2l thermal conductivities 2K and K are connected end to end. If cross sectional areas of two rods are eual, then equivalent thermal conductivity of the system is .
A(5/6)KB1.5KC1.2KD(8/9)K Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement II: For two cylindrical rods of identical size and different thermal conductivity K1 and K2 connected in series, the equivalent thermal conductivity K is given by 2K=1K1+1K2AStatement I is true, Statement II is true and Statement II is the correct explanation for statement I.BStatement I is true, statement II is true and statement II NOT the correct explanation for Statement ICStatement I is true, Statement II is false.DStatement I is false, statement II is true.
An iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the juction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
 .
.
View SolutionAn iron bar (L1=0.1m,A1=0.02m2,K1=79Wm−1K−1) and a brass bar (L2=0.1m,A2=0.02m2,K2=109Wm−1K−1) are soldered end to end as shown in fig. the free ends of iron bar and brass bar are maintained at 373 K and 273 K respectively. Obtain expressions for and hence compute (i) the temperature of the junction of the two bars, (ii) the equivalent thermal conductivity of the compound bar and (iii) the heat current through the compound bar.
 .
.
View SolutionFind equivalent thermal conductivity in the following cases:
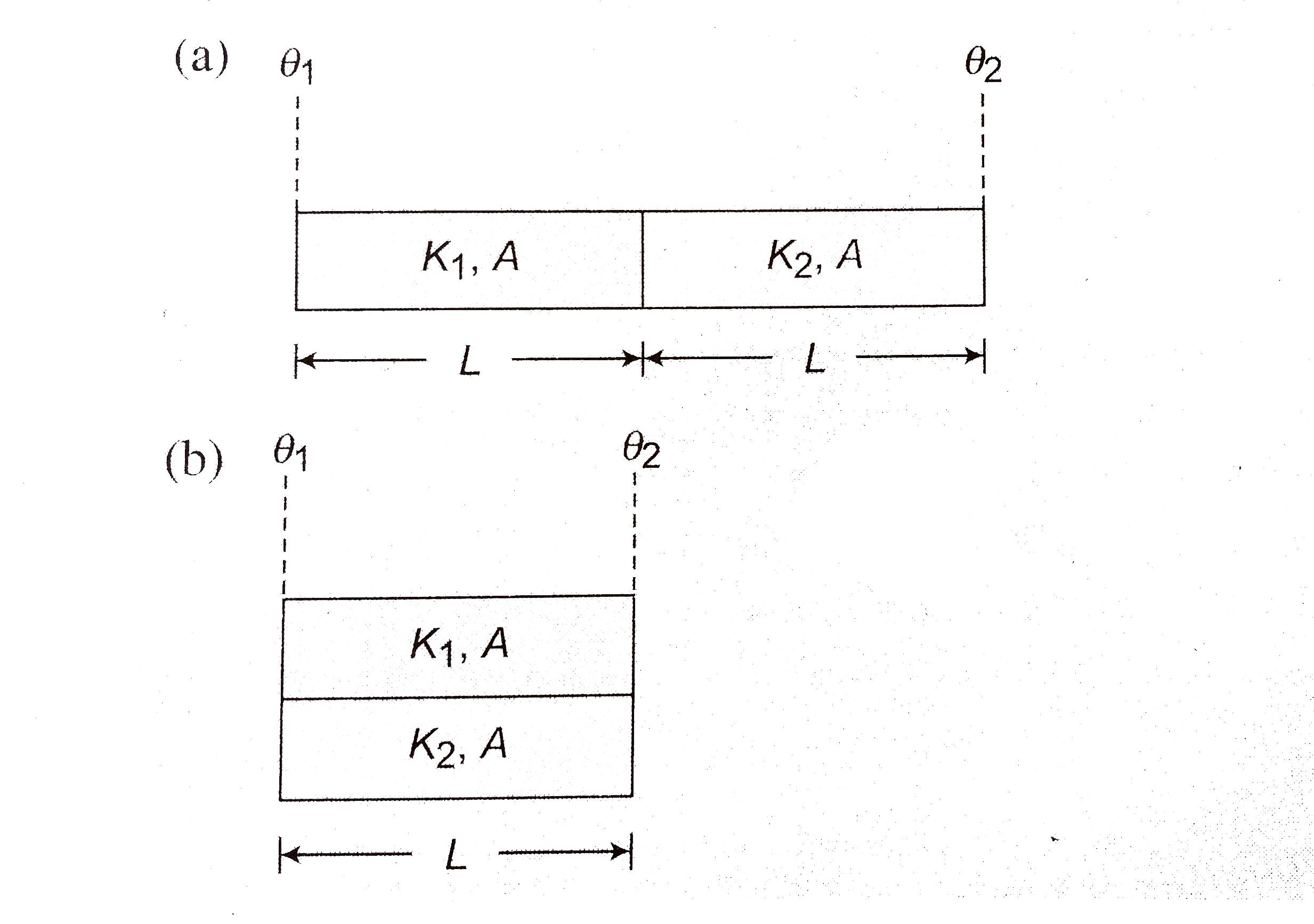

View Solution
Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement II: For two cylindrical rods of identical size and different thermal conductivity K1 and K2 connected in series, the equivalent thermal conductivity K is given by 2K=1K1+1K2
View Solution
Statement I: Two solid cylindrical rods of identical size and different thermal conductivity K1 and K2 are connected in series. Then the equivalent thermal conductivity of two rods system is less than that value of thermal conductivity of either rod.
Statement II: For two cylindrical rods of identical size and different thermal conductivity K1 and K2 connected in series, the equivalent thermal conductivity K is given by 2K=1K1+1K2
View Solution
