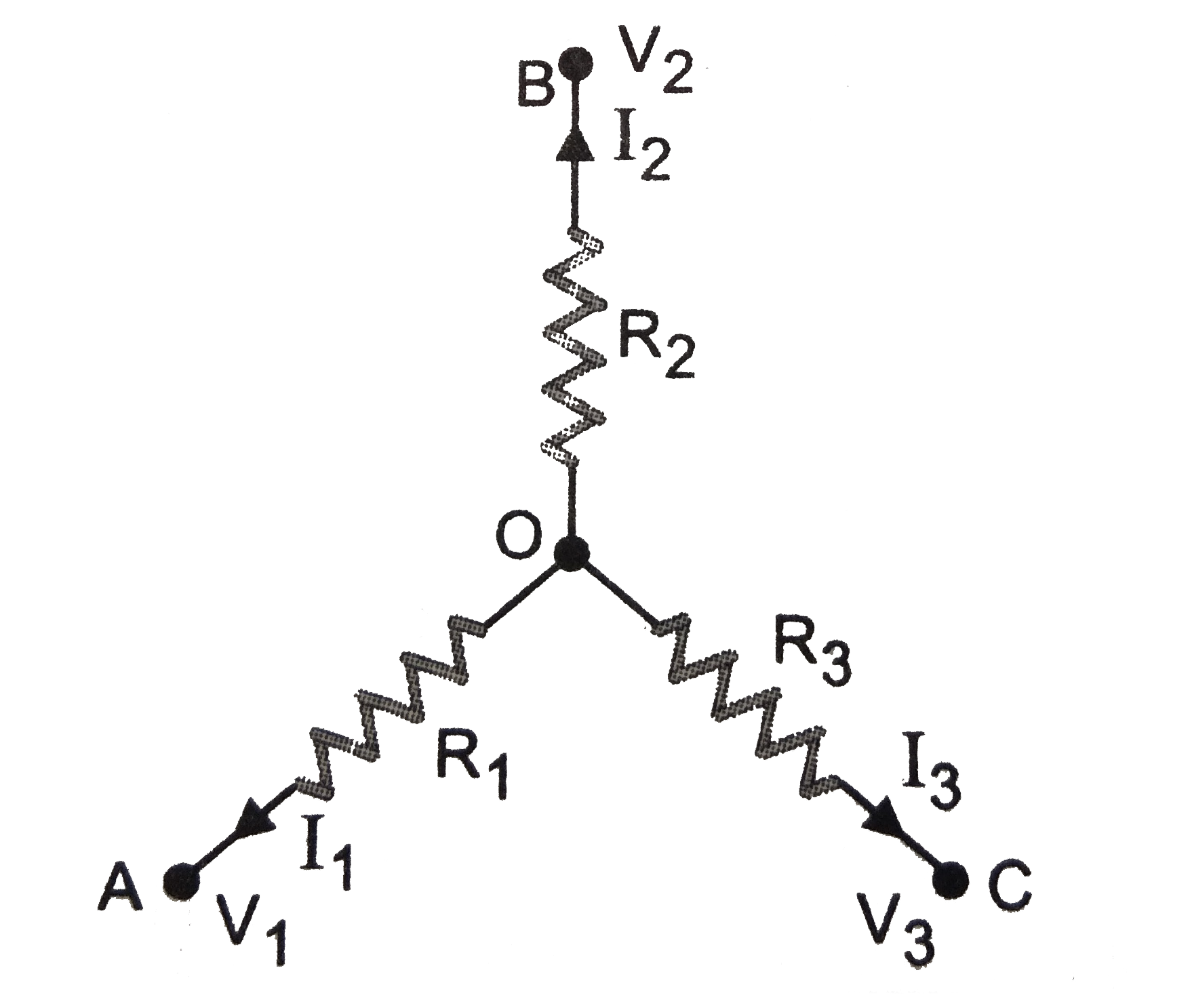
A circuit has a section ABC if the potential at point A,BandC are V1,V2andV3 respectively , calculate the potential at point O
V1+V2+V3
[V1R1+V2R2+V3R3][1R1+1R2+1R3]−1
zero
[V1+V2+V3R1+R2+R3](R1+R2+R3)
The correct Answer is:B
Applying juction rule −I1−I2−I3=0
i.e., I1+I2+I3=0…(i)
Let, V0 bet the potential at point O. By Ohm's law for resistance, R1,R2andR3 respectively, we get
(V0−V1)=I1R1,(V0−V2)=I2R2and(V0−V3)=I3R3
orI1=(V0−V1)R1,I2=(V0−V2)R2,I3=(V3−V3)R3
So substituting these values of I1,I(2)andI3 in eq. (i) , we get
V0[1R1+1R2+1R3]−[V1R1+V2R2+V3R3]=0
V0=[V1R1+V2R2+V3R3][1R1+1R2+1R3]−1
Topper's Solved these Questions
- BOOK - NCERT FINGERTIPSCHAPTER - CURRENT ELECTRICITYEXERCISE - Wheatstone Bridge6videos
CURRENT ELECTRICITY
- BOOK - NCERT FINGERTIPSCHAPTER - CURRENT ELECTRICITYEXERCISE - Meter Bridge4videos
CURRENT ELECTRICITY
- BOOK - NCERT FINGERTIPSCHAPTER - CURRENT ELECTRICITYEXERCISE - Cell In Series And In Parallel3videos
CURRENT ELECTRICITY
- BOOK - NCERT FINGERTIPSCHAPTER - COMMUNITCATION SYSTEMSEXERCISE - HOTS10videos
COMMUNITCATION SYSTEMS
- BOOK - NCERT FINGERTIPSCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Assertion And Reason15videos
DUAL NATURE OF RADIATION AND MATTER
Similar Questions
The arrangement shows a part of complete circuit. The potentials at point A and B are V1 and V2 respectively . Find the potential at point P.
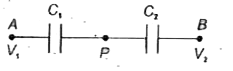
Strategy : The two capacitors C1 and C2 are connected in series . Therefore the charge on both of the capacitors is same . Let the potential at P is V .View SolutionThree capacitors C1,C2 and C3 are connected as shown in, The potentials of P,Q, and R are V1,V2, and V3, respectively. Find the potential V0 at the functionO.
 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
Three resistance are joined together to form a letter Y, as shown in figure. If the potentials of the terminals A,B and C are 6V,3V and 2V respectively, then the potential of the point O will be
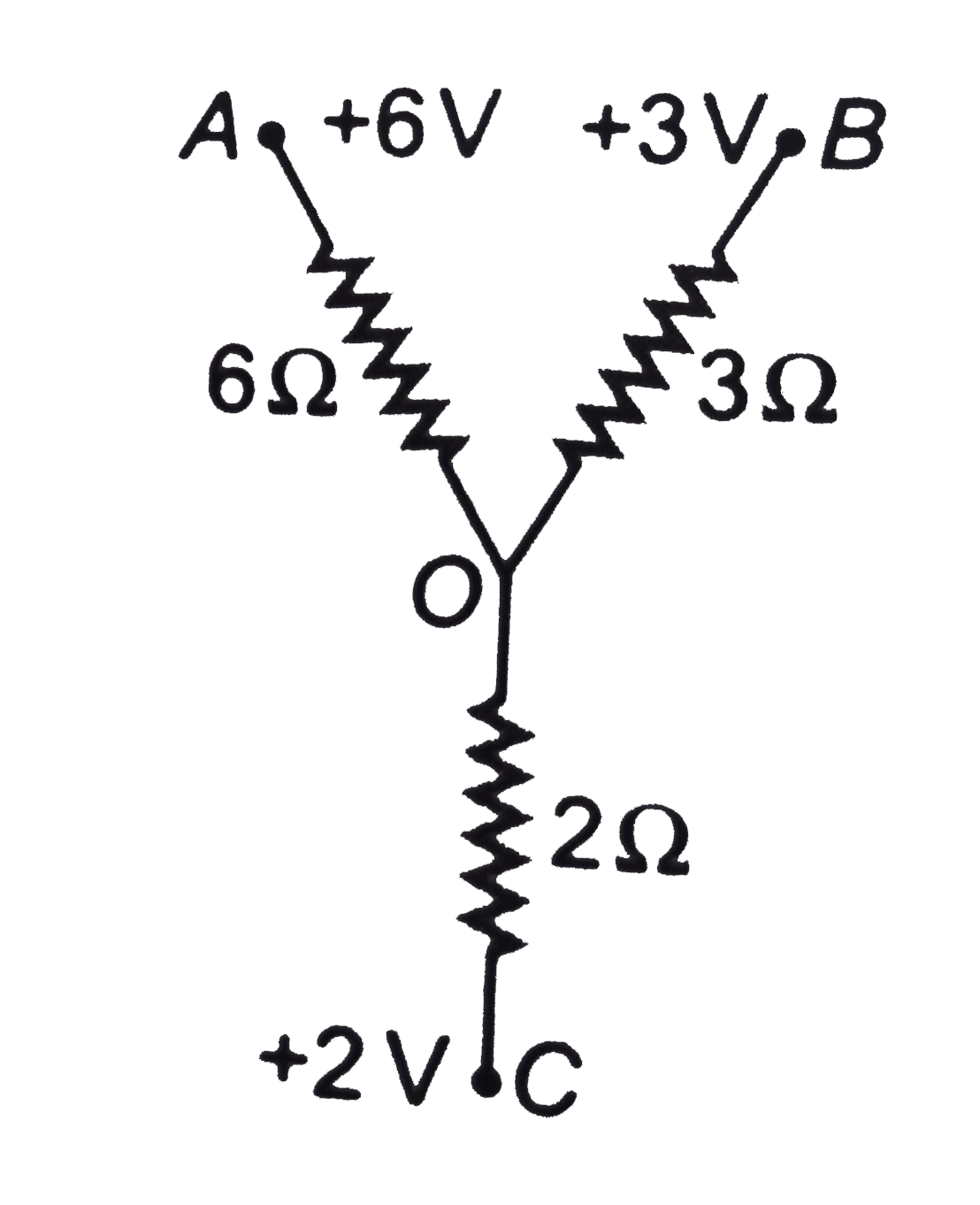 A4VB3VC2.5VD0V
A4VB3VC2.5VD0V - Question 2 - Select One
Three uncharged capacitors of capacities C1,C2 and C3 are connected as shown in the figure to one another and the potentials V1,V2 and V3 respectively. Then the potential at O will be
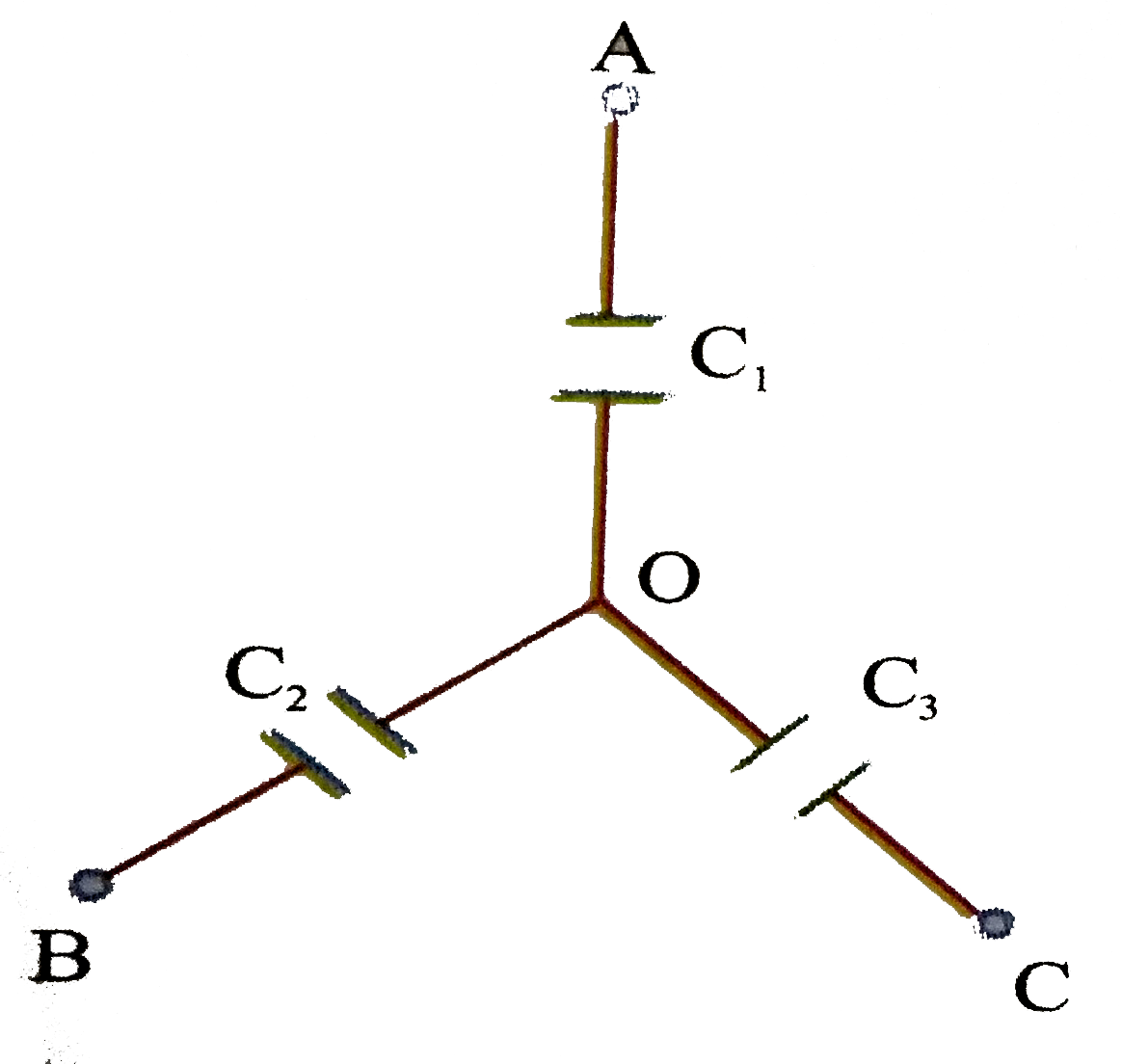 .AV1C1+V2C2+V3C3C1+C2+C3BV1+V2+V3C1+C2+C3CV1(V2+V3)C1(C2+C3)DV1V2V3C1C2C3
.AV1C1+V2C2+V3C3C1+C2+C3BV1+V2+V3C1+C2+C3CV1(V2+V3)C1(C2+C3)DV1V2V3C1C2C3 - Question 3 - Select One
In the given network, the potential at point O is (Given VO=Vs=18V)
 A9VB780/47VC680/43VDnone of these
A9VB780/47VC680/43VDnone of these
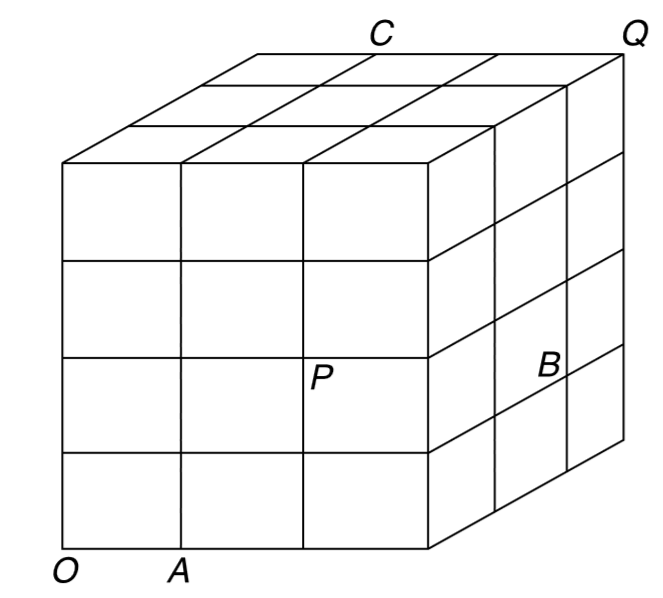
A uniform electric field exists in a region of space. Potential at potential O,A,B and C are V0=0 and VA=−1V,VB=−6V and VC=−3V respectively. Alll the cubes shown in fig have side length of 1m. ltbr> (a). Find VP−VQ
(b). Find the smallest distance of a point from O where the potential is −2V
 View Solution
View SolutionFind the potential difference between points A and B (VB−VA) in the network
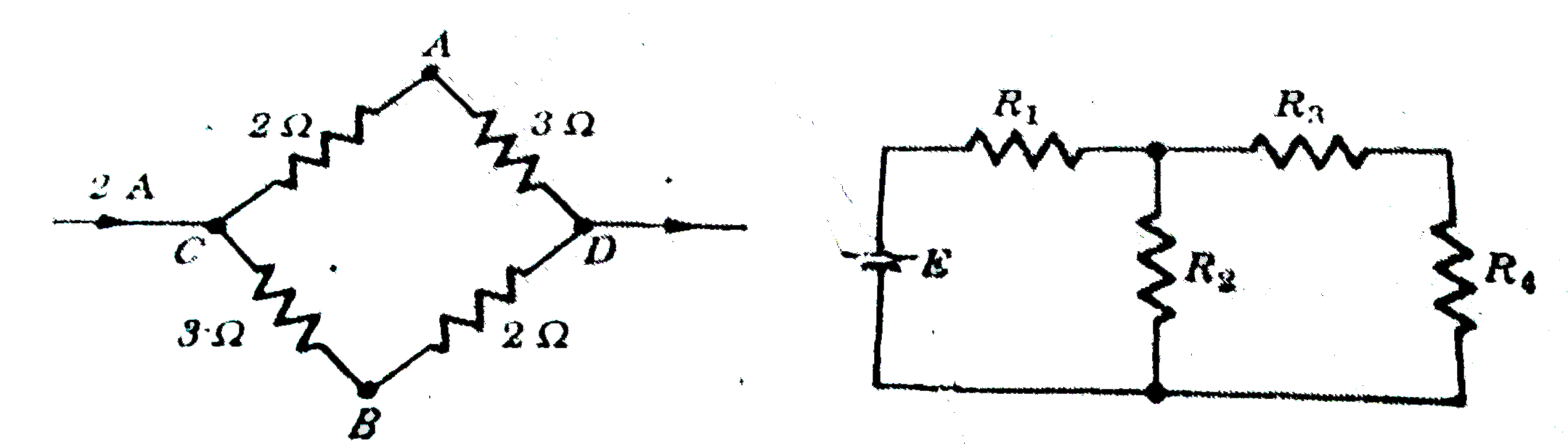 View Solution
View Solution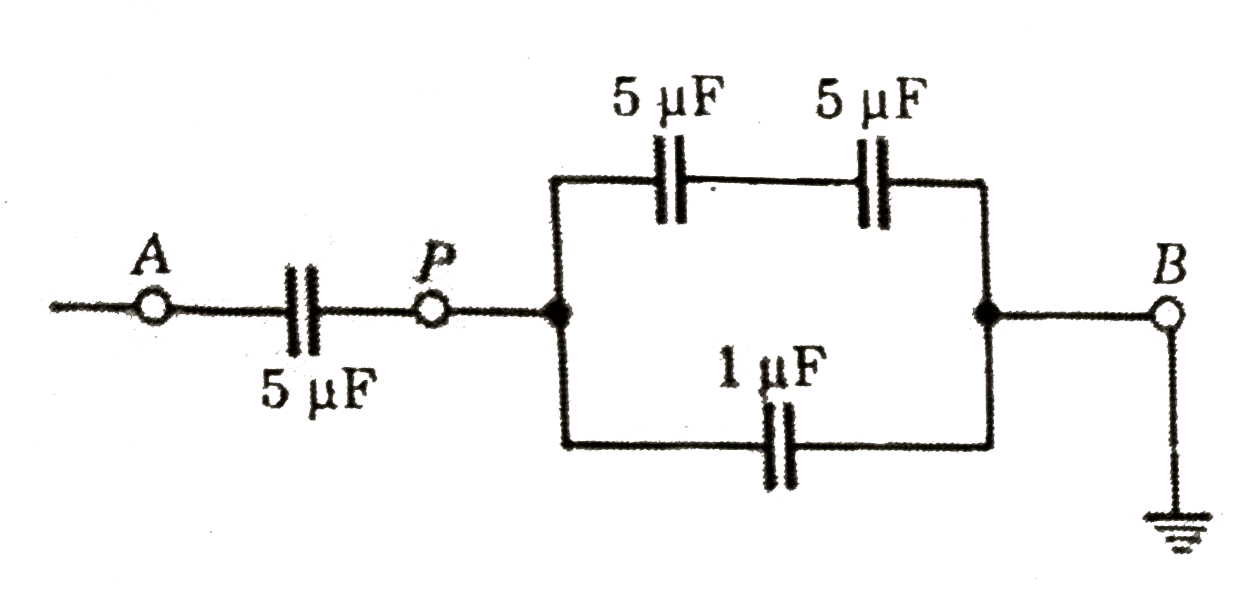
In the circuit shown in figure. If point B is earthed and A is kept at 1500 V, then calculate the potential at the point P.View SolutionShown a part of an electric circuit, The potentials at the points a,b,and c are 30V,12V,and 2V respectively.Find the currents through the three resistors.
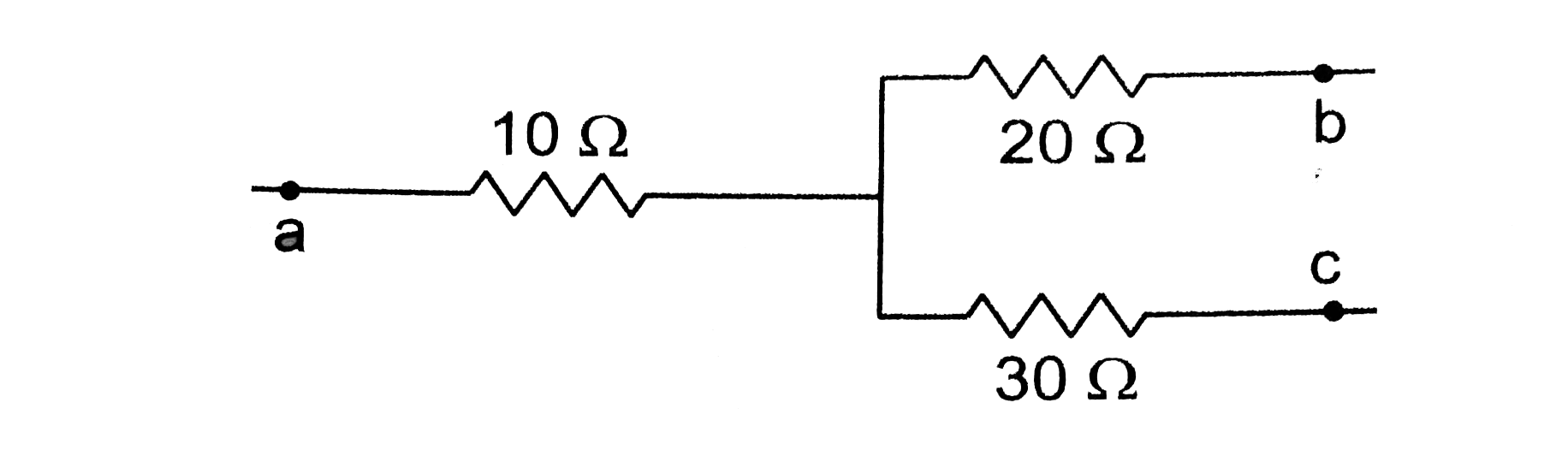 View Solution
View SolutionFigure shown three points A,B and C in a region of unifrom electric field →E. The line AB is perpendicular and BC is parallel to the field lines. Then which of the following holds good. Where VA,VB and VC represenet the electric potential at points A,B and C respectively
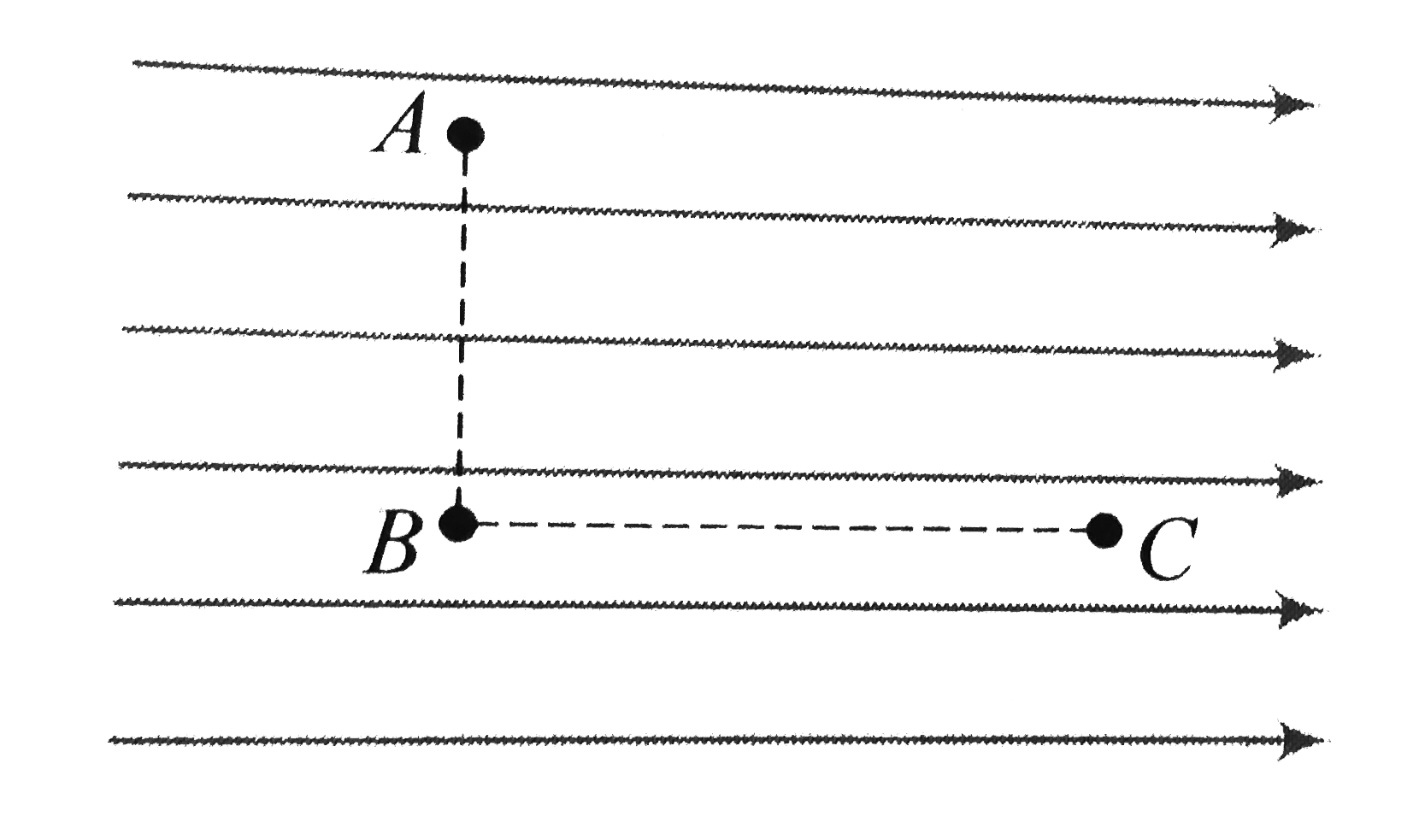 View Solution
View Solution

