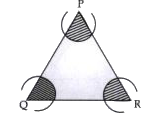
In figure arcs have been drawn with radii 14 cm each and with centres P, Q and R. Find the area of the shaded region .

Video Solution

Text Solution

Verified by Experts

Given that radii of each arc ( r) = 14cm
Now, area of the sector with central $∠ P = \frac{∠ P}{360^{\circ}} \times π r^{2}$
= $\frac{∠ P}{360^{\circ}} \times π \times {(14)}^{2} c m^{2}$
[ $∴$ area of any sector with central angle $θ$ and radius r = $\frac{π r^{2}}{360^{\circ}} \times θ$ ]
Area of the sector with central central angle = $\frac{∠ Q}{360^{\circ}} \times π r^{2} = \frac{∠ Q}{360^{\circ}} \times π \times {(14)}^{2} c m^{2}$
and area of the sector with central angle R = $\frac{∠ R}{360^{\circ}} \times π r^{2} = \frac{∠ R}{360^{\circ}} \times π \times {(14)}^{2} c m^{2}$
Therefore, sum of the areas (in $c m^{2}$ ) of three sectors
= $\frac{∠ P}{360^{\circ}} \times π \times {(14)}^{2} + \frac{∠ θ}{360^{\circ}} \times π \times {(14)}^{2} + \frac{∠ R}{360^{\circ}} \times π \times {(14)}^{2}$
= $\frac{∠ P + ∠ Q + ∠ R}{360} \times 196 \times π = \frac{180^{\circ}}{360^{\circ}} \times 196 π c m^{2}$ [since, sum of all interior angles in any triangle is $180^{\circ}$ ]
= $98 π c m^{2} = 98 \times \frac{22}{7}$
= $14 \times 22 = 308 c m^{2}$
Hence, the required area of the shaded region is $308 c m^{2}$ .

|

Updated on:21/07/2023

Class 10 MATHS AREAS RELATED TO CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Three circles with centres A, B and C and with unit radii touch each other at O, P and Q. Find the area of the shaded region .

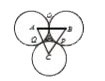A0.16 sq. units
B1.21 sq. units
C0.03 sq. units
D0.32 units

NCERT EXEMPLAR-AREAS RELATED TO CIRCLE-Long Answer Type Questions

Home
Ask Doubt
Profile