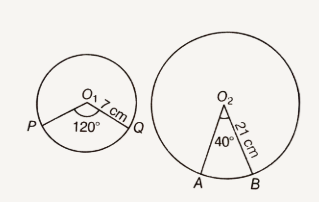
The central angles of two sectors of circles of radii 7 cm and 21 cm are respectively $120^{\circ} and 40^{\circ}$ . Find the areas of the two sectors as well as the lengths of the corresponding arcs. What do you observe ?

Video Solution

Text Solution

Verified by Experts

Let the lengths of the corresponding arc be $l_{1} and l_{2}$ .
Given that, radius of sector $P O_{1} Q P$ = 7 cm
and radius of sector $A O_{2} B A = 21 c m$
Central angle of the sector $P O_{1} Q P = 120^{\circ}$
and central angle of the sector $A O_{2} B A = 40^{\circ}$
= $\frac{π r^{2}}{360^{\circ}} \times θ = \frac{π {(7)}^{2}}{360^{\circ}} \times 120^{\circ}$
= $\frac{22}{7} \times \frac{7 \times 7}{360^{\circ}} \times 120$
= $\frac{22 \times 7}{3} = \frac{154}{3} c m^{2}$
and area of the sector with central angle $O_{2}$
= $\frac{π r^{2}}{360^{\circ}} \times θ = \frac{π {(21)}^{2}}{360^{\circ}} \times 40^{\circ}$
= $\frac{22}{7} \times \frac{21 \times 21}{360^{\circ}} \times 40^{\circ}$
= $\frac{22 \times 3 \times 21}{9} = 22 \times 7 = 154 c m^{2}$
Now, corresponding arc length of the sector $P O_{1} Q P$
= Central angle $\times$ Radius of the sector
= $120^{\circ} \times 7 \times \frac{π}{180^{\circ}}$ [ $∵ θ = \frac{l}{r} and 1^{\circ} = \frac{π}{180^{\circ}} R$ ]
= $\frac{2}{3} \times 7 \times \frac{22}{7}$
= $\frac{44}{3} c m$
and corresponding arc lengh of the sector $A O_{2} B A$
Central angle $\times$ Radius of the sector
= $40^{\circ} \times 21 \times \frac{π}{180^{\circ}}$ [ $∴ θ = \frac{l}{r} and 1^{\circ} = \frac{π}{180^{\circ}} R$ ]
= $\frac{2}{9} \times 21 \times \frac{22}{7}$
= $\frac{2}{3} \times 22 = \frac{44}{3} c m$
Hence, we observe that arc length of two sectors of two different circles may be equal but their area need not be equal.

|

Updated on:21/07/2023

Class 10 MATHS AREAS RELATED TO CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the area of the sector of a circle of radius 5 cm, if the corresponding arc length is $3.5$ cm.
A $7$ $c m^{2}$
B $8.75$ $c m^{2}$
C $8.25$ $c m^{2}$
D $7.25$ $c m^{2}$

NCERT EXEMPLAR-AREAS RELATED TO CIRCLE-Long Answer Type Questions

Home
Ask Doubt
Profile