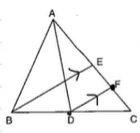
In the adjoining figure. AD and BE and BE are two medians of ΔANC.if DF||BE,then prove thatCG=14AC.
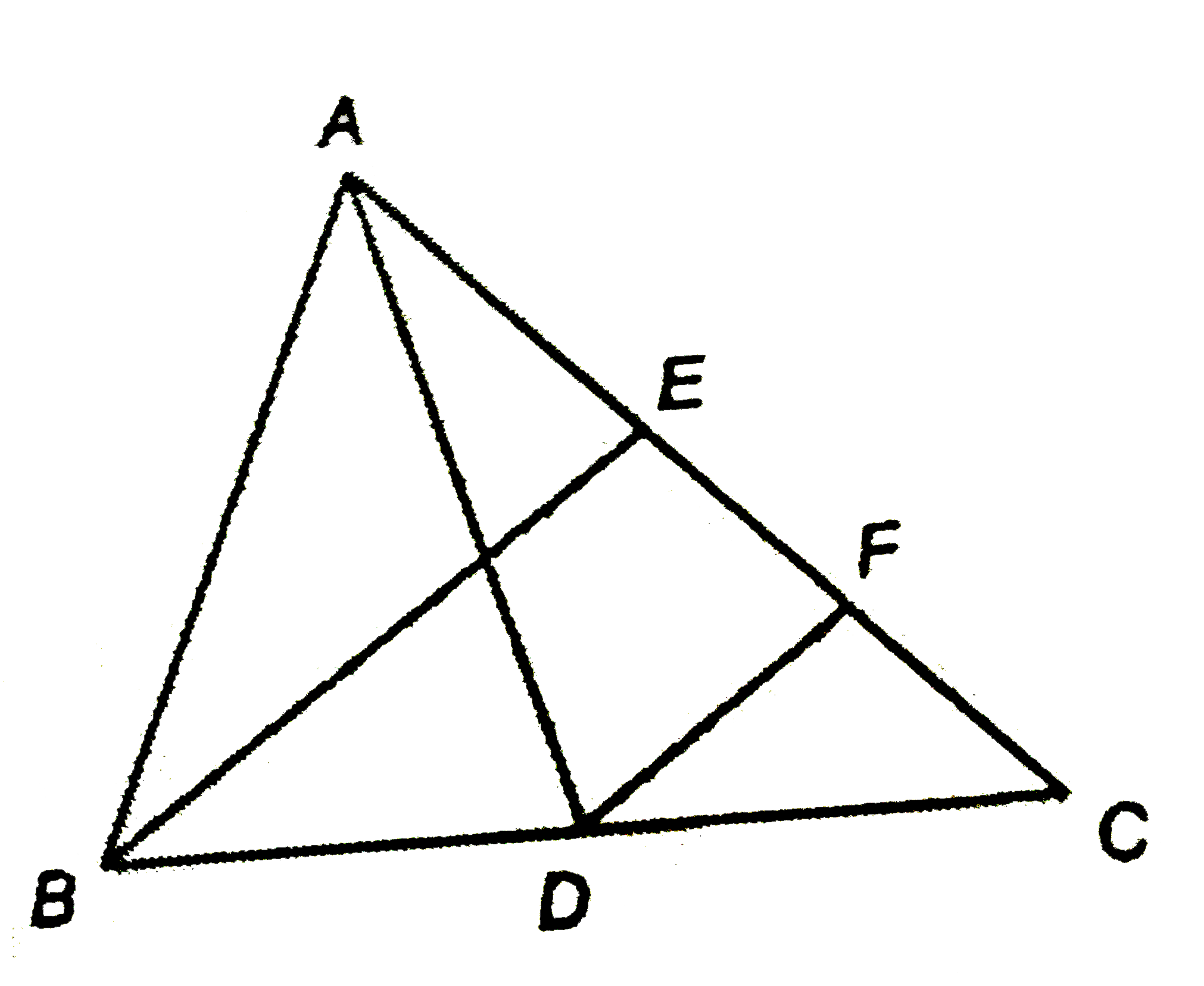
E is the mid-point of line AC.
∴CE=12AC ...(1)
In ΔABE,
Since, D is the mid-point of CB and DF||BE
∴F will be the mid-point of CE. (coverse of mid-point theorem)
⇒ CF=12CE
⇒ CF=12×12AC [from(1)]
⇒ CF=14AC
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar11videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a29videos
QUADRILATERALS
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)10videos
PROBABILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise10videos
STATISTICS
Similar Questions
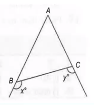
In the adjoining figure,AB=AC.Find the value of x
View SolutionIn the adjoining figure, find AC . (FIGURE)
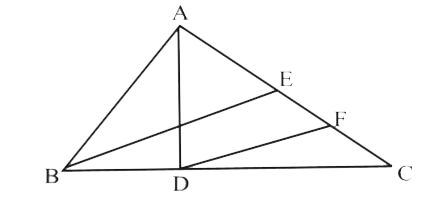
View SolutionIn the given figure AD and BE are the medians of ΔABC and BE || DF . Prove that CF=1/4AC.
 View Solution
View SolutionIn the adjoining figure, x>y, Prove that AB>AC
 View Solution
View SolutionIn the adjoining figure, BC = ED, then, prove that ΔABC≅ΔFDE.
 View Solution
View SolutionIn the adjoining figure, AD=DC and bisects ∠ADC. Prove that ΔADB≅ΔCDB.
 View Solution
View SolutionIn theadjoining figure, ∠DAB=∠ABC and AD=BC prove that BD=AC.
 View Solution
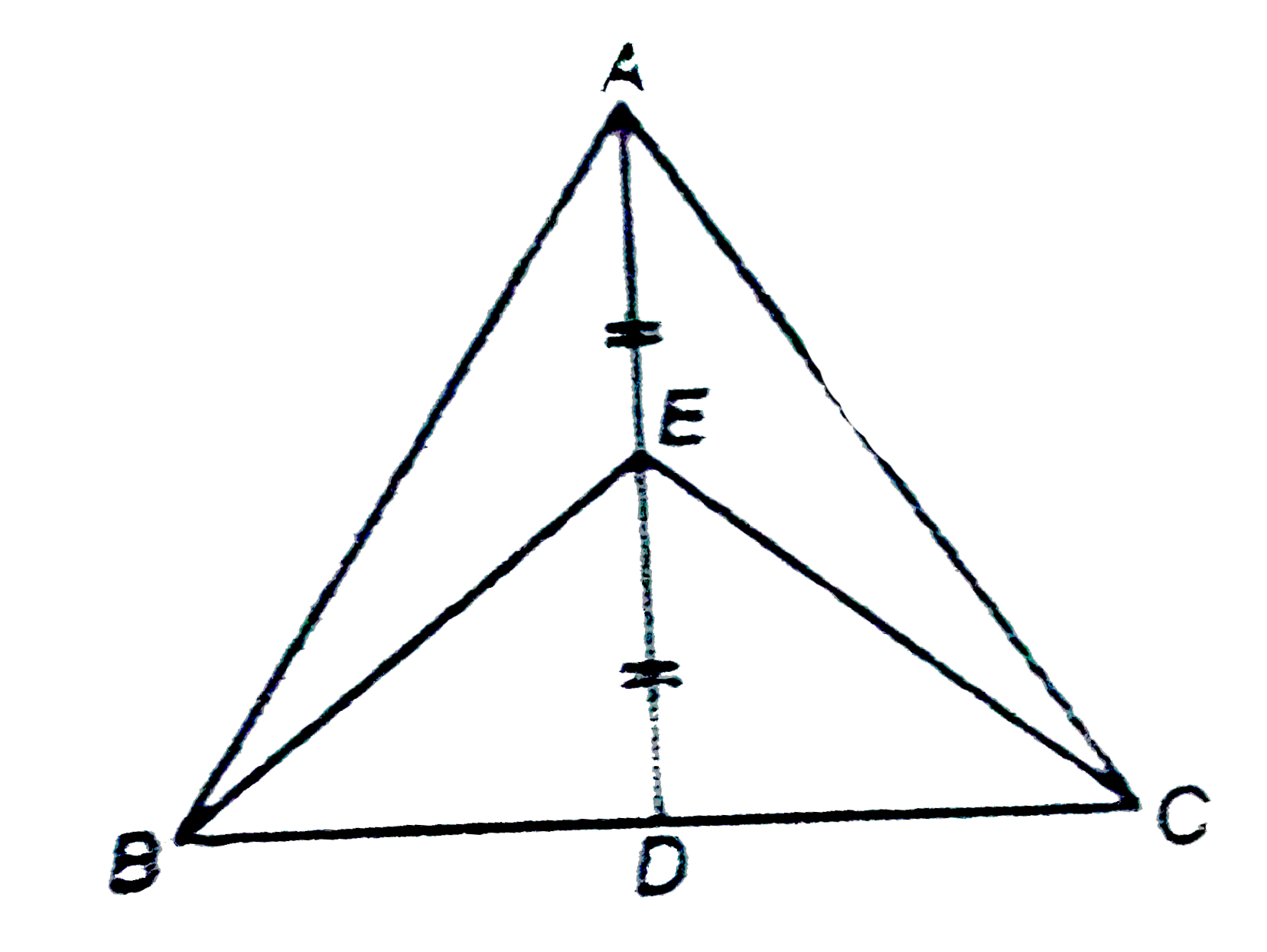
View SolutionIn Figure, AD, and BE are medians of ABC and BE∣∣DF. Prove that CF=14AC.
 View Solution
View SolutionIn the adjoining figure, BD = DC and AE = ED. Prove that
area of ΔACE=14 area of ΔABC
 View Solution
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.
 View Solution
View Solution

