There are 175 students in a class, out of which 100 students opt Maths, 70 opt Physics and, 23 opt Physics and Chemisty, 28 opt Chemistry and Maths and 18 opt of all three subjects. Now find each of the following :
No. of students who opt why only Maths
(ii) No. of students who opt only Physics
(iii) No. of students who opt only Chemistry
(iv) No. of students who opt Physics and Chemisty but not Maths
(v) No. of students who opt Maths and Physics but not Chemistry
(vi) No. of students who opt only one subject
(viii) No. of students who opt atleast one subject
(viii) No. of student who do not opt any subject.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

Let A = set of students opted Maths
B = set of student opted Physics
C = set of students opted Chemistry
and U = set of students of the class
Given that n(U)=175,n(A)=100,n(B)=70,n(C)46
n(A∩B)=30,n(B∩C)=23,n(C∩A)=28,n(A∩B∩C)=18
(i) No. of students opted Maths only
=n(A∩B'∩C')
=n[A∩(B∪C)']
=n(A)−n[A∩(B∪C)]
[∵n(A∩B')=n(A)−n(A∩B)]
=n(A)−n[(A∩B)∪(A∩C)]
=n(A)−[n(A∩B)+n(A∩C)−n(A∩B∩C)]
=100−30−28+18=60.
(ii) No. of students opted Physics only
=n(B∩A'∩C')
=n(B)−[n(B∩C)+n(B∩A)−n(A∩B∩C)]
=70−(23+30−18)=35.
(iii) No. of students opted Chemistry only
n(C∩A'∩B')
=n(C)−[n(C∩A)+n(C∩B)−n(A∩B∩C)]
=46−(28+23−18)=13.
(iv) No. of students opted Physics and Chemistry but not Maths
=n(B∩C∩A')
=n(B∩C)−n(B∩C∩A)
=23−18=5.
(v) No. fo student opted Maths and Physics but not Chemistry
n(A∩B∩C')=n(A∩B)−n(A∩B∩C)
=30−18=12
(vi) No. of students taken only one subject
=n(A)+n(B)+n(C)−2n(A∩B)−2n(B∩C)−2n(C∩A)+3n(A∩B∩C)
=100+70+46−2(30+23+28)+3×18
=216−162+54=108.
(vii) No. of students taken atleast one subject
n(A∪B∪C)=n(A)+n(B)+n(C)−n(A∩B)−n(B∩C)−n(C∩A)+n(A∩B∩C)
=100+70+46−(30+23+28)+18
=234−81=153
(viii) No. of students taken no subject =n(U)−n(A∪B∪C)=175−153=22
Second method : Here M = set of students taken Maths
P = set of students taken Physics
C = set of students taken Chemistry
Consider the Venn diagram
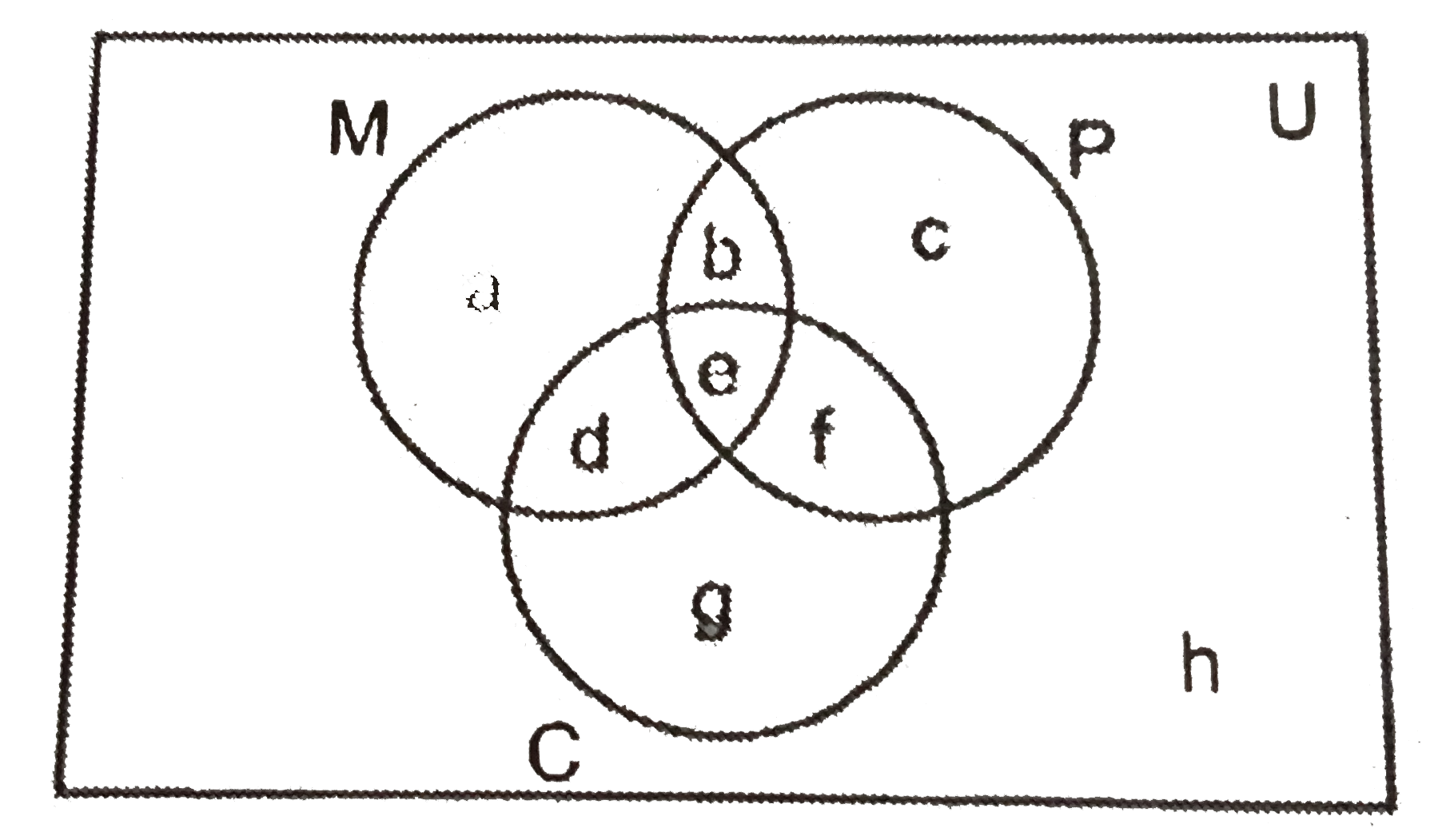
ocr_image
n(M)=a+b+d+e=100
n(P)=b+c+e+f=70
n(C)=d+e+f+g=46
n(M∩P)=b+e=30
n(P∩C)=e+f=23
n(M∩C)=d+e=28
n(M∩P∩C)=r=18
n(U)=a+b+c+d+e+f+g+h
=175
On solving
e=18
d+18=28⇒d=10
18+f=23⇒f=5
b+18=30⇒b=12
n(C)=d+e+f+g=46
⇒10+18+5+g=46
⇒g=13
n(P)=b+c+e+f=70
⇒12+c+18+5=70
⇒c=35
n(M)=a+b+d+e=100
⇒a+12+10+18=100
⇒a=60
and n(U)=a+b+c+d+e+f+g+h
=175
⇒60+12+35+10+18+5+13+h=175
⇒h=22
Now, (i) No. of students taken Maths only =a=60.
(ii) No. of students taken Physics only = c = 35
(iii) No. of student taken Chemisty only = g = 13.
(iv) No. of students taken Physics and Chemistry but not Maths = f = 5
(v) No. of students taken Maths and Physics but not Chemistry = b = 12
(vi) No. of students taken only one subject
=a+c+g
=60+35+13=108
(vii) No, of students taken atleast one subject
=a+b+c+d+e+f+g
=60+12+35+10+18+5+13
=153
(viii) No. of student taken no subject
=h=22.

Updated on:21/07/2023
|
Class 11MATHSSETS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • In a class 20 students opted for Physics, 17 for Maths,12 for both Physics and Maths and 10 students for other subjects. The class contains how many students ?

    A52
    B35
    C50
    D42

  • In a class , 40 student like Maths, 50 students like Physics and 60 students like Chemistry. 30 students like both Maths and Physics, 20 students like both Physics and Chemistry and none of them like both Maths of Chemistry . Find the total number of students who like only Maths, only Physics and only Chemistry.

    A10
    B40
    C50
    D30