x-अक्ष के अनुदिश गति करने के लिए स्वतन्त्र की स्थितिज ऊर्जा, सीमाओं −∞≤x≤+∞ के अंतर्गत, U(x)=k[1−e−x2] द्वारा दी जाती है,जहाँ k उपयुक्त विमाओं वाला धन नियतांक है। तब
यदि दो द्रव्यमान m1 तथा m2 स्प्रिंग की सहायता से जुड़े हैं तथा क्षैतिज सतह पर गति करने के लिए स्वतन्त्र हैं, तो आवर्तकाल
![x-अक्ष के अनुदिश गति करने के लिए स्वतन्त्र की स्थितिज ऊर्जा, सीमाओं - oo le x le + oo के अंतर्गत, U ( x) = k [ 1 -e^(-x^(2))] द्वारा दी जाती है,जहाँ k उपयुक्त विमाओं वाला धन नियतांक है। तब यदि दो द्रव्यमान m(1) तथा m(2) स्प्रिंग की सहायता से जुड़े हैं तथा क्षैतिज सतह पर गति करने के लिए स्वतन्त्र हैं, तो आवर्तकाल T = 2pi sqrt(( mu )/( k )) यहाँ, mu = समानित( Reduced) द्रव्यमान = ( m(1) m(2))/(m(1) + m(2))](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_HIN_41Y_JEE_PHY_SP_C08_E01_006_Q01.png)
T=2π√μk
यहाँ, μ= समानित( Reduced) द्रव्यमान =m1m2m1+m2
मूल बिंदु से दूर के बिंदुओं पर कण अस्थायी संतुलन में हैं
x के किसी भी परिमित अशून्य मान के लिए, कण पर मूल बिंदु से दूर एक बल लगता है
यदि इसकी कुल यांत्रिक ऊर्जा K/2 है , तो इसकी न्यूनतम गतिज ऊर्जा मूल बिंदु पर है
x=0 से अल्प विस्थापन के लिए गति सरल आवर्त है
The correct Answer is:A
U(x)=k(1−e−x2)
यह U का x2 के साथ एक आरोही चरघातांकी (exponential) रेखाचित्र प्रदर्शित करने वाला समीकरण है। मूल बिंदु पर स्थितिज ऊर्जा U न्यूनतम गतिज ऊर्जा अधिकतम )तथा कण पर कार्य करने वाला बल शून्य है क्योंकि F=−dUdx=−(U−x ग्राफ का ढाल ) =0
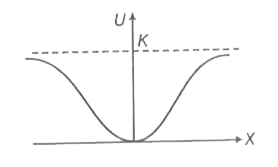
इस प्रकार मूल बिंदु एक स्थायी साम्यावस्था ( stable equilibrium ) की स्थिति है। अतः कण विस्थापन के सभी मानों के लिए x = 0 के परितः सरल आवर्त गति करेगा। अतः विकल्प (d) सही है।
( a), (b) , ( c ) विकल्पों के गलत होने के निम्न कारण हैं -
( a) साम्यावस्था में F=−dUdx=0 अर्थात U -x ग्राफ का ढाल x=0 तथा x=±∞ पर शून्य होना चाहिए। अब इन सभी साम्यावस्थाओं में स्थायी साम्यावस्था की स्थिति वह है जहाँ U,(x=0) न्यूनतम हो। जहाँ U अधिकतम है वहां अस्थायी साम्यावस्था की स्थिति है। उदासीन संतुलन (neutral equilibrium ) की स्थिति वह है। जहाँ U नियत है ( यहां x=±∞ ) इसलिए विकल्प (a) सही नहीं है।
(b) x के किसी भी निश्चित अशून्य मान के लिए, बल मूल बिंदु की और कार्यरत होगा क्योंकि मूल बिंदु स्थायी साम्यावस्था की स्थिति में है। इस प्रकार विकल्प (b) गलत है।
( c ) मूल बिंदु पर स्थितिज ऊर्जा न्यूनतम है, अतः गतिज ऊर्जा अधिकतम होगी। इस प्रकार विकल्प (c ) भी सही नहीं है।
Topper's Solved these Questions
- सरल आवर्त गति BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सरल आवर्त गति EXERCISE - बहुविकल्पीय प्रश्न II (एक से अधिक विकल्प सही हैं )
6 Videos
- सरल आवर्त गति BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सरल आवर्त गति EXERCISE - रिक्त स्थानों की पूर्ति कीजिए
2 Videos
- शुद्धगतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - शुद्धगतिकी EXERCISE - विश्लेषणात्मक प्रश्न
9 Videos
- सामान्य भौतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - सामान्य भौतिकी EXERCISE - विश्लेषणात्मक प्रश्न
9 Videos
Similar Questions
एक रैखिक सरल आवर्ती दोलित्र का बल नियतांक 2×106 न्यूटन / मी तथा आयाम 0.01 मी है, इसकी कुल यांत्रिक ऊर्जा160 जूल है। इसकी
View Solutionदो सरल आवर्त गतियाँ y1=10sin(3πt+π4) तथा y2=5[sin3πt+√3cos3πt] समीकरणों से प्रदर्शित की जाती है। इनके आयामों का अनुपात............. है, इन गतियों के आवर्तकाल.............. हैं।
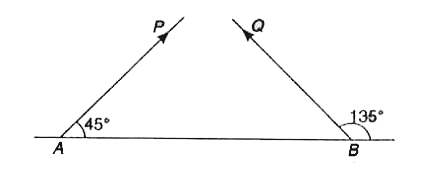
View Solutionभूमि पर स्थित दो बिंदुओं A तथा B से दो कण P तथा Q जिनके द्रव्यमान क्रमशः 20 ग्राम तथा 40 ग्राम है, प्रक्षेपित किये जाते है। P तथा Q के प्रारंभिक वेग क्षैतिज AB से चित्रानुसार क्रमशः 45∘ तथा 135∘ के कोण बनाते है। प्रत्येक कण की प्रारंभिक चाल 49 मी/से तथा दुरी AB ,245 मी है। दोनों कण समान ऊर्ध्वाधर तल में गति करते हुए संघट्ट करते है। संघट्ट के पश्चात P अपने पथ पर लोट आता है। Q की स्थिति की गणना कीजिए जहाँ वह भूमि पर लटकाता है। संघट्ट के बाद कण Q को भूमि पर पहुंचने में कितना समय लगता है? (g=9.8 मी/से 2)
View Solutionनीचे दी गई राशियों के MKS पद्धति में मात्रक बताइए।
(i) यंग प्रत्यास्थता गुणांक
(ii) चुम्बकीय प्रेरण
(iii) लेन्सों की क्षमता
View Solutionk के किस मान के लिए रेखाएँ y=(2+√3)x+4 तथा y=kx+6 एक दूसरे से 60∘ के कोण पर झुकी है ?
View Solutionदर्शाइए की बिंदु x=2at1+t2 तथा y=a(1−t2)1+t2 जहाँ a स्थिर राशि है t प्राचल है तथा −1≤t≤1,t के प्रत्येक मान के लिए वृत्त पर स्थित है ।
View Solutionx के किन मानों के लिए फलन f(x)=x1+x2 वर्धमान तथा ह्रासमान है।
View Solutionx के किन मानो के लिए फलन f(x)=(x)(x2+1 वर्धमान तथा हस्यमान है ?
View Solutionफलन के लिए रोल प्रमेय की सत्यता की जाँच कीजिए
f(x)=⎧⎪⎨⎪⎩x2+10≤x≤1यदि3−x1<x≤2
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionयदि समीकरण x2+x+1=0 के मूल a,b हैं तथा x2+px+q=0 के मूल हैं, ab,ba तो p+q का मान है
View Solutionश्रवण कौशल को विकसित करने के लिए उपयुक्त प्रणाली है
View SolutionM_(1)=56 वाली गैस 1 के T_(1) और M_(2) = 44 वाली गैस 2 के T_(2) के मध्य क्या संबंध होगा, यदि गैस 1 की औसत चाल, गैस 2 की अति संभाव्य गति के बराबर है?
View Solutionउच्च तापमान पर एक साम्यावस्था क्रियाकारकां की ओर विस्थापित हो जाती है इस साम्यावस्था के लिए In K तथा 1//T के मध्य कौन सा आलेख सही है?
View Solutionसक्रियण ऊर्जा की गणना के लिए log k बनाम 1/T के बीच का आरेख किसके द्वारा दिखाया गया है?
View Solutionलोहे से बने जहाज की तली की रक्षा करने के लिए सबसे सुविधाजनक विधि है:
View Solution
