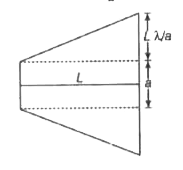
एक पिन - होल कैमरा की लम्बाई L है तथा छिद्र की त्रिज्या a है। उस पर λ तंगदैर्ध्य के समान्तर प्रकाश आपतित है। छिद्र के सामने वाली सतह केपीआर बने स्पॉट के विस्तार छिद्र के ज्यामितीय आकर तथा विवर्तन के कारण हुए विस्तार के कुल योग है। इस स्पॉट के न्यूनतम bmin आकर तब होगा जब
a=λ2L तथा bmin=(2λ2L)
a=√λL तथा bmin=(2λ2L)
a=√λL तथा bmin=√4λL
a=λ2L तथा bmin=√4λL
The correct Answer is:C
विवर्तन में , प्रथम निम्नष्ठ sinθ=λa
इसलिए बिन्दु का आकर b=2a+2Lλa ...(i)
तब , बिन्दु का न्यूनतम आकर हम पाते है
∂b∂a=0⇒1−Lλa2=0
⇒a=√λL ...(ii)
इसलिए bन्यूनतम=2√λL+2√λL
[समी (ii) का मान समी (i) में रखने पर]
bन्यूनतम=4√λL
अतः बिन्दु कि त्रिज्या 42√λL=√4λL
Topper's Solved these Questions
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - बहुविकल्पीय प्रश्न II (केवल एक विकल्प सही है)
19 Videos
- तरंगे BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - तरंगे EXERCISE - सत्य / असत्य
3 Videos
- चुम्बकत्व BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - चुम्बकत्व EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार (अनुच्छेद iii )
2 Videos
- द्रव्यमान केंद्र और सवेगBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - द्रव्यमान केंद्र और सवेगEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार
3 Videos
Similar Questions
y-दिशा के अनुदिश विस्थापन को प्रदर्शित करने बलि तरंग की समीकरण y=10−4sin(60t+2x) है , जहाँ x तथा y मीटर में तथा t सेकण्ड में है। यह समीकरण प्रदर्शित करती है
View Solutionसमान ताप पर हाइड्रोजन गैस (γ=75) तथा हीलियम गैस (γ=53) में ध्वनि के वेगों का अनुपात √215 है।
View Solutionदर्शाए चित्रानुसार धातु की एक पतली आयताकार पट्टी में एकसमान विद्युत धारा । धनात्मक दिशा में प्रवाहित हो रही है। पट्टी की लम्बाई, चौड़ाई तथा मोटाई क्रमश: 1, wतथा d हैं। पट्टी पर धनात्मक दिशा में एकसमान चुम्बकीय क्षेत्र B लगाया गया हैं। जिसके कारण आवेशवाहक :-दिशा की ओर विक्षेपित होते हैं। परिणामतः सतह PORS पर आवेशवाहकों का संचयन होता है तथा PORS के सामने के फलक पर बराबर किन्तु विपरीत आवेश आ जाता है। तब एक विभवान्तर --दिशा के साथ विकसित होता है। आवेशवाहकों का यह संचयन तब तक जारी रहता है जब तक कि चुम्बकीय बल, वैद्युत बल से सन्तुलित नहीं हो जाता। विद्युत धारा का प्रवाह इलेक्ट्रॉनों के द्वारा तथा पट्टी की अनुप्रस्थ काट पर एकसमान है
Q एक ही चालक पदार्थ की दो अलग-अलग पट्टियों (1 तथा 2) लें। उनकी लम्बाइयाँ बराबर हैं, चौडाइयाँ क्रमश:w1 एवं w2 तथा मोटाइयाँ क्रमश: d1 तथा d2 हैं। दो बिन्दु K तथा Mx-y तल के समान्तर आमने-सामने के फलकों पर स्थित हैं। पट्टियों । तथा 2 में K तथा M के बीच विभवान्तर क्रमश: V1 तथा V2 हैं। तब उनमें बहने वाली एक दी गई विद्युत धारा / तथा एक दी गई चुम्बकीय क्षेत्र की तीव्रता B के लिए सही कथन है (हैं)
View Solutionहर प्रकार की गतिकीय समस्याओं के निश्लेषण के लिए कला-समष्टि चित्रा (Phase space diagrams) का उपयोग किया जाता है। प्रारम्भिक दशा, स्थिति व संवेग में बदलाव होने पर इनका उपयोग चालन में उत्पन्न बदलावों को समझने में बहुत उपयोगी है। यहाँ हम एकविमीय सरल गतिकीय निकायों की बात करते हैं। इनके लिए कला-समष्टि समतल है जिसमें स्थिति X-अक्ष पर तथा संबेग Y-अक्ष पर रखते हैं, तब कुला-समष्टि चित्र इस समतल में एक x(t)-p(t) वक्र होगा। वक्र पर तीर समय बढ़ने की दिशा को दर्शाता है।
उदाहरण के लिए, स्थिर वेग से चल रहे कण के लिए कला- समष्टि चित्रा है, सरल रेखा है, जिसे चित्र में दिखाया गया है। चिह्न परिपाटी में स्थिति या संवेग को ऊपर (या दाहिने) ओर धनात्मक तथा नीचे (या बाई) ओर ऋणात्मक माना जाता है।
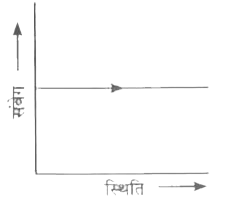
1. जमीन से ऊपर की ओर फेंकी गई गेंद का कला-समष्टि चित्रा है।
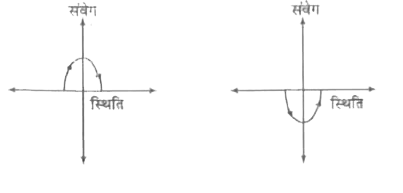
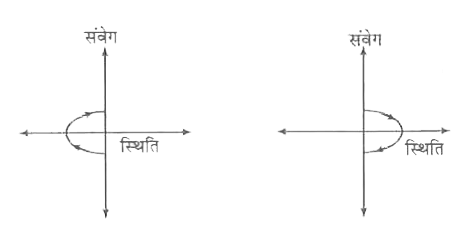
View Solutionचन्द्रमा पर गुरुत्वाकर्षण के कारण त्वरण है ?
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionरेखा तथा वृत्त के स्पर्श बिंदु के निर्देशांक ……………. है ।
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। इस बात की क्या प्रायिकता है की ग्यारह कदमो के पशचात वह व्यक्ति शुरुआती बिन्दु से एक कदम दूर है?
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionएक घन के विकर्ण की लम्बाई 12√3 सेमी है। घन के कोर की लम्बाई .............होगी।
View Solutionप्रतिबिंबो की संख्या #!#दर्पण की न्यूनतम लम्बाई #!#दर्पण के घुर्णन के कारण प्रतिबिंब पर प्रभाव
View Solutionएक काय केंद्रित घनीय जालक का निर्माण B के खोखले गोलों से किया गया है। ठोस A के गोले, B के खोखले गोलों में उपस्थित है। A की त्रिज्या, B की त्रिज्या की आधी है। एकक कोष्ठिका में, A द्वारा अनअधिधारित B के गोलों के कुल आयतन और एकक कोष्ठिका के आयतन का अनुपात क्या है?
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solutionउच्च तापमान पर एक साम्यावस्था क्रियाकारकां की ओर विस्थापित हो जाती है इस साम्यावस्था के लिए In K तथा 1//T के मध्य कौन सा आलेख सही है?
View Solutionएक आदर्श गैस के लिए चक्र के सिरों पर दिखाए गए परिवर्तन की एक श्रेणी के माध्यम से किया गया कुल कार्य निम्न के बराबर है:
View Solution
