Prove that:
.2C2+3C2+4C2+…..+n+1C2=16n(n+1)(n+2)
N/a
Topper's Solved these Questions
- BINOMIAL THEOREMBOOK - NAGEEN PRAKASHANCHAPTER - BINOMIAL THEOREMEXERCISE - Exercise 8E
20 Videos
- BINOMIAL THEOREMBOOK - NAGEEN PRAKASHANCHAPTER - BINOMIAL THEOREMEXERCISE - Exercise 8F
20 Videos
- BINOMIAL THEOREMBOOK - NAGEEN PRAKASHANCHAPTER - BINOMIAL THEOREMEXERCISE - Exercise 8C
28 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATION BOOK - NAGEEN PRAKASHANCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATION EXERCISE - MISCELLANEOUS EXERCISE
20 Videos
Similar Questions
Prove that:
.2C2+3C2+4C2+…..+n+1C2=16n(n+1)(n+2)
View SolutionProve that:
.2C2+3C2+4C2+…..+n+1C2=16n(n+1)(n+2)
View SolutionIf (1+a)n=.nC0+.nC1a+.nC2a2+..+.nCnan, then prove that
.nC1+2.nC2+3.n3C3+...+n.nCn=n.2n−1.
View SolutionIf (1+a)n=.nC0+.nC1a+.nC2a2+..+.nCnan, then prove that
.nC1+2.nC2+3.n3C3+...+n.nCn=n.2n−1.
View SolutionIn C0,C1C2….Cn are the binomial coefficients in the expansion of (1+x)n then prove that :
(i)C20−C21+C22−C23+…..+(−1)n.C2n
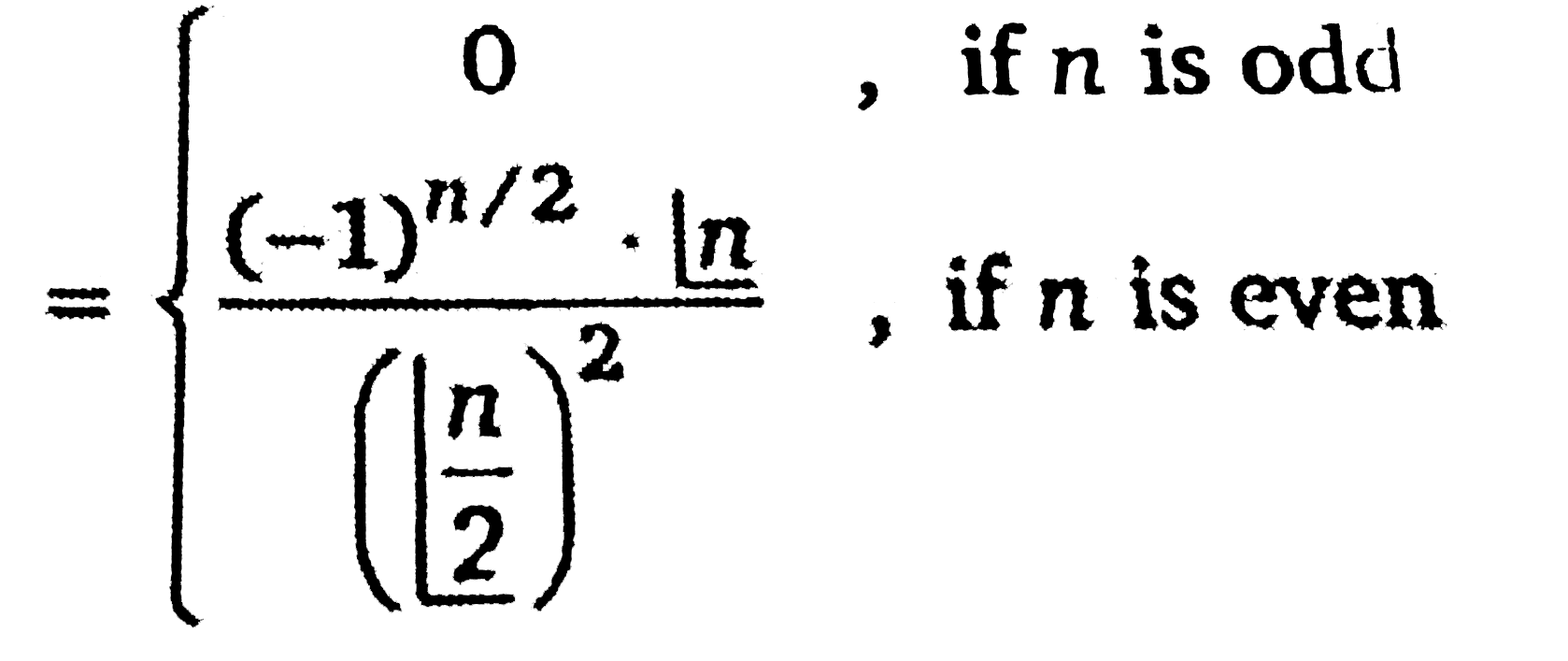
(ii)C0C1+C1C2+C2C3+....+Cn−1Cn
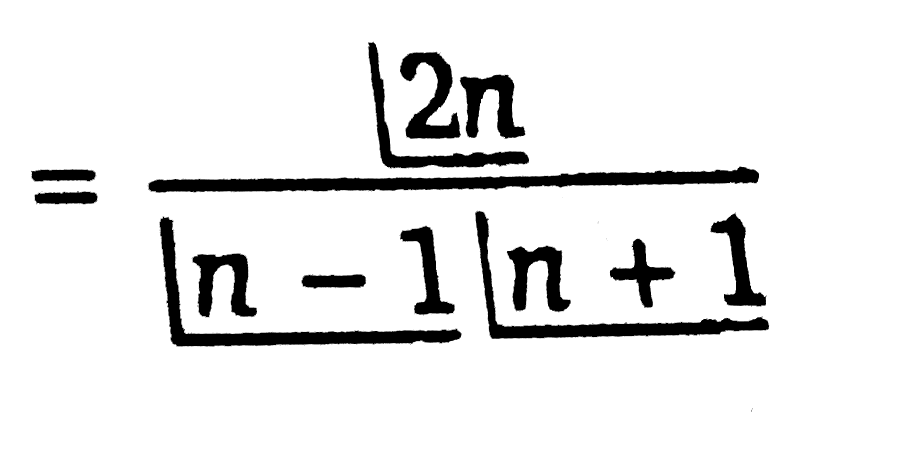
View SolutionIf C0,C1,C2………Cn are the binomial coefficient in the expansion of (1+x)n then prove that:
C20+C21+C22+……..+C2n=∣2–n|n––|n––
View SolutionIf C0,C1,C2………Cn are the binomial coefficient in the expansion of (1+x)n then prove that:
C20+C21+C22+……..+C2n=∣2–n|n––|n––
View SolutionIf (1+x)n=C0+C1x+C2x2
+…+Cnxn, prove that +32⋅C3+…+n2⋅Cn
12⋅C1+22⋅C2=n(n+1)⋅2n−2 .
View SolutionIf (1+x)n=C0+C1x+C2x2
+…+Cnxn, prove that 12⋅C1+22⋅C2+32⋅C3+…+n2⋅Cn =n(n+1)⋅2n−2 .
View SolutionProve that (.2nC0)2−(.2nC1)2+(.2nC2)2−….+(.2nC2n)2=(−1)n.2nCn
View Solution
