Three letters are dictated to three persons and an envelope is addressed to each of them, the letters are inserted into the envelopes at random so that each envelope contains exactly one letter. Find the probability that at least one letter is in
The correct Answer is:N/a
No. of ways to insert 3 letters into 3 envelops
=⌊3=6
The letter an envelopes can be arrange in the following manners.
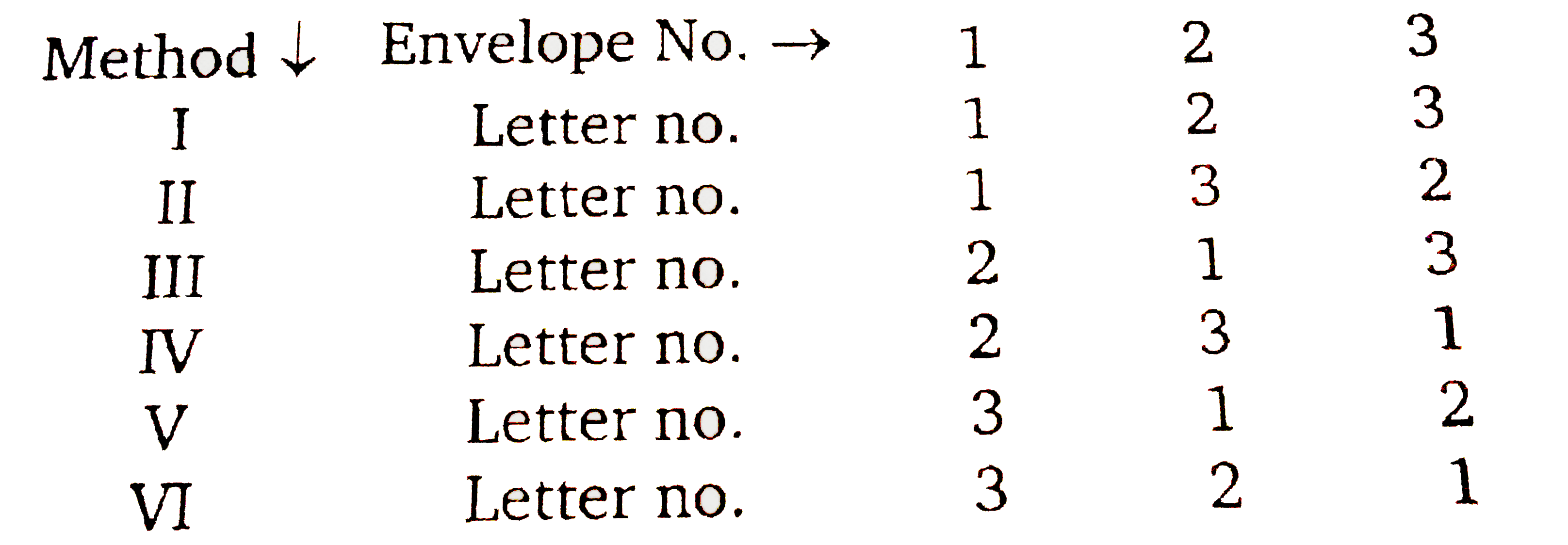
Here in I,II,III,VI methods, at least one letter is in proper envelope.
∴ No. of ways to arrange at least one letter in correct envelope =4
∴ Probability that atleast one letter is in correct envelope
=46=23
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - NCERT QUESTIONS43videos
PROBABILITY
- BOOK - NAGEEN PRAKASHANCHAPTER - PRINCIPLE OF MATHEMATICAL INDUCTIONEXERCISE - Exercise 429videos
PRINCIPLE OF MATHEMATICAL INDUCTION
- BOOK - NAGEEN PRAKASHANCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE12videos
RELATIONS AND FUNCTIONS
Similar Questions
There sre three letters asnd three envelopes. Find the total number of wys in which letters can be put into the envelopes so that each envelope has only one letter.
View SolutionThere are 6 letters and 6 addressed envelopes. Find the probability that at least one letter goes into the wrong envelope.
View Solution
Knowledge Check
- Question 1 - Select One
Ravi writes 5 letters and addresses 5 envelopes. If the letters are placed in the envelopes at random, then the probability that a least one letter goes into the wrong envelope is
A1120B119120C160D115120 - Question 2 - Select One
There are 4 envelopes corresponding to 4 letters. If the letters are placed in the envelopes at random, probability that all the letters are not placed in the right envelopes is
A1824B2324C1724D724 - Question 3 - Select One
There are 3 letters and 3 envelopes. Find the number of ways in which all letters are put in the wrong envelopes
A4B2C6D8
If four letters are placed into 4 addressed envelopes at random, the probability that exactly two letters will go wrong is
View Solutionn letters are written to n different persons and addresses on the n envelopes are also written. If the letters are placed in the envelopes at random, the probability that at least one letter is not placed in the right envelope, is (A) 1−1n (B) 1−12n (C) 1−1n2 (D) 1−1n!
View SolutionThree letters are written to different persons and their addresses are also written on three envelopes. Letters are put at random in the envelopes. Then the probability that at least one letter is put in the correct envelope, is ______.
View SolutionThere are 4 letters and 4 addressed envelopes. Find the probability that all the letters are not dispatched in right envelopes.
View SolutionThere are 3 letters and 3 envelopes. Find the number of ways in which all letters are put in the wrong envelopes
View Solution

