Consider a semicircle of radius 1 unit constructed on the diameter AB, and let O be its centre. Let C be a point on AO such that AC : CO = 2:1. Draw CD perpendicular to AO with D on the semicircle. Draw OE perpendicular to AD with E on AD. Let OE and CD intersects at H. Then DH equals

A

$\frac{1}{\sqrt{5}}$

B

$\frac{1}{\sqrt{3}}$

C

$\frac{1}{\sqrt{2}}$

D

$\frac{\sqrt{5} - 1}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:c

E is mid point of AD.
theta $cos 2 θ = \frac{1}{3} \Rightarrow {cos}^{2} θ - 1 = \frac{1}{3}$
${cos}^{2} θ = \frac{2}{3}$
$cos θ \frac{\sqrt{2}}{\sqrt{3}}$
$sin θ = \sqrt{1 - \frac{2}{3}} = \frac{1}{\sqrt{3}}$
$\frac{E D}{1} = \frac{1}{\sqrt{3}}$
$D H = E D sec θ$
$\frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{2}}$
$\frac{1}{\sqrt{2}}$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

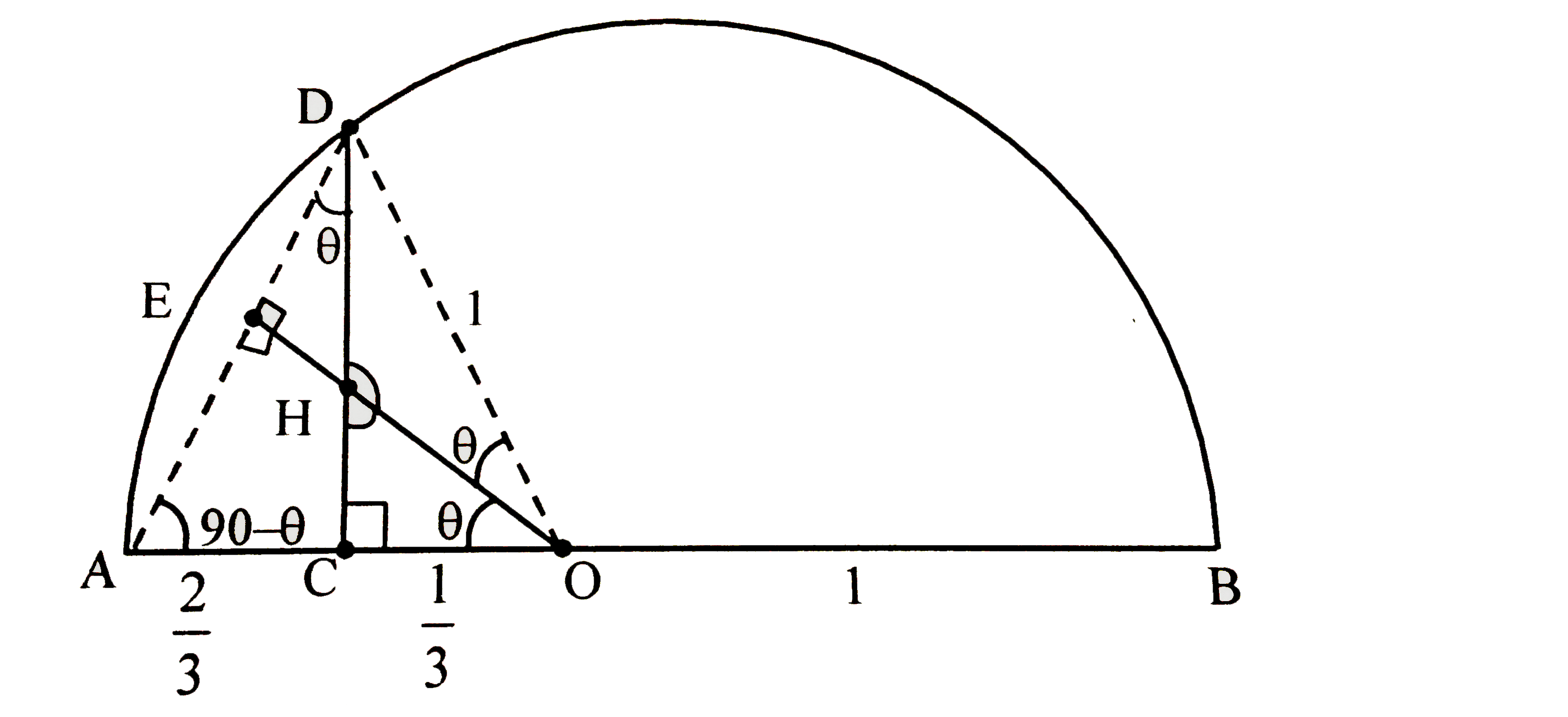
Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Suppose AB is a diameter of a circle, whose centre is at O and C be any point on the circle. If CD is perpendicular to AB and CD = 12 cm, AD = 16 cm, then BD is equal to
A10 cm
B12 cm
C8 cm
D9 cm
Question 2 - Select One
The middle point of A (1, 2) and B (x, Y) is C (2, 4). If BD is perpendicular to AB such that CD=3 unit, then what is the length BD ?
A $2 \sqrt{2}$ unit
B2 unit
C3 unit
D $3 \sqrt{2}$ unit
Question 3 - Select One
The middle point of A (1, 2) and B (x, y) is C (2, 4). If BD is perpendicular to AB such that CD = 3 unit, then what is the length BD ?
A $2 \sqrt{2}$ unit
B2unit
C3 unit
D $3 \sqrt{2}$ unit

KVPY PREVIOUS YEAR-KVPY-Matematics

Home
Ask Doubt
Profile