चित्र में दिखाये गये दो सदिशों →A और →B के बीच का कोण θ है। इनके परिणामी सदिश का परिमाण तथा दिशा उनके परिमाणों तथा θ के पद मे निकालिए। 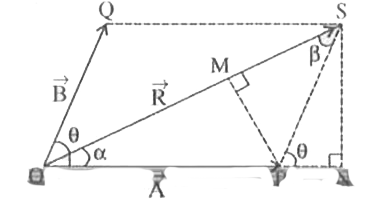
चित्र के अनुसार माना −−→OP तथा −−→OQ दो सदिशों →A तथा →B को व्यक्त करते हैं जिसके बीच का कोण θ है। तब सदिश योग के समांतर चतुर्भुज नियम द्वारा हमें परिणामी सदिश →R प्राप्त होगा, जिसे चित्र में −−→OS द्वारा दिखाया गया है।
→R=→A+→B
चित्र में SN⊥OP और PM⊥OS
∴OS2=ON2+SN2
लेकिन ON=OP+PN=A+Bcosθ
∵cosθ=PNSP∴PN=Bcosθ
sinθ=SNSP=SNB SN=Bsinθ
∴OS2=(A+Bcosθ)2+(Bsinθ)2
अथवा R2=A2+2ABcosθ+B2cos2θ+B2sin2θ
R2=A2+2ABcosθ+B2(cos2θ+sin2θ)
R2=A2+2ABcosθ+B2×1 sin2θ+cos2θ=1
⇒R2=A2+B2+2ABcosθ
=R=√A2+B2+2ABcosθ………1
ΔOSN में SN=PSsinθ=Bsinθ
अतएव Rsinα=Bsinθ∴Rsinθ=Bsinα…….2
इसी प्रकार PM=Asinα=Bsinβ
अथवा Asinβ=Bsinα……..3
समीकरण 2 तथा 3 को शामिल करने पर
Rsinθ=Asinβ=Bsinα………4
समीकरण 4 को ज्या नियम कहते हैं।
समकोण त्रिभुज ONS से
tanα=NSON=NSOP+PN
=BsinθA+Bcosθ
⇒tanα=BsinθA+Bcosθ…….5
Topper's Solved these Questions
- BOOK - SANJEEV PUBLICATIONCHAPTER - समतल रेखा में गतिEXERCISE - पाठ्यपुस्तक के प्रश्न32videos
समतल रेखा में गति
- BOOK - SANJEEV PUBLICATIONCHAPTER - समतल रेखा में गतिEXERCISE - अन्य महत्तवपूर्ण प्रश्न (बहुचयनात्मक प्रश्न)12videos
समतल रेखा में गति
- BOOK - SANJEEV PUBLICATIONCHAPTER - मात्रक एवं मापन EXERCISE - गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न33videos
मात्रक एवं मापन
- BOOK - SANJEEV PUBLICATIONCHAPTER - सरल रेखा में गति EXERCISE - गत वर्षों की विभिन्न प्रतियोगी परीक्षाओं में पूछे गये प्रश्न17videos
सरल रेखा में गति
Similar Questions
निम्नलिखित भौतिक राशियों में से बताइए कि कौन सी सदिश हैं और कौन सी अदिश
आयतन, द्रव्यमान, चाल, त्वरण, घनत्व, मोल संख्या, वेग, कोणीय आवृत्ति, विस्थापन, कोणीय वेग।02:47View Solutionयदि सदिश →A की दिशा में एकांक सदिश ˆn है तो
03:16View Solutionसमीकरण P=a−t2bx में P दाब, x दूरी तथा t समय है, b की विमा होगी -
04:06View Solutionएक बिल्ली एकसमान चाल vu से X से Y तक जाती है और एकसमान चाल vd से Y से X पर वापस आती है | इसमें उसकी औसत चाल होगी -
05:32View Solutionयदि →a,→b,→c तीन असमतलीय एकांक सदिश है तथा →a×(→c×→b)=→b+→c√2 तो →a और →b के मध्य कोण है -
02:07View Solutionयदि →a.→b=0 तथा →a+→b,→b के साथ 60° का कोण बनाते हैं तो |→a| बराबर है
02:17View Solutionयदि ¯u और ¯v एकांक सदिश हों तथा उनके बीच का न्यून कोण θ हो, तो 2¯u×3¯v एक एकांक सदिश होगा :
04:51View Solutionसदिश ¯a=α¯i+2¯j+β¯k, सदिशों ¯b=¯i+¯j तथा ¯c=¯j+¯k के तल में स्थित है तथा ¯b और ¯c के बीच के कोण का समद्विभाजन करता है, तो निम्न में से कौनसा α और β के सम्भावित मान प्रदान करता है ?
04:32View Solutionसदिश →a और →b दो मात्रक सदिश है तथा इनके बीच का कोण α है। यदि →a+→b भी एक मात्रक सदिश है तो α का मान होगा -
04:23View Solutionयदि दो सदिशों →a और →b के बीच का कोण θ है तो →a.→b≥0 होगा। यदि -
04:55View Solutionदिये गये चित्र में, OA और OB वृत्त की त्रिज्याएँ है। इनके बीच का कोण 100∘ का है। यदि बाहरी बिंदु P से PA और PB वृत्त की स्पर्श रेखाएं हो, तो ∠APB का मान है:
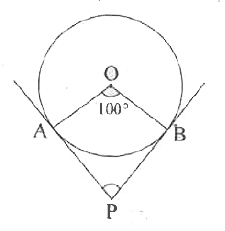 02:59View Solution
02:59View Solution→a,→b,→c क्रमश 3,4,5 परिमाण के सदिश है। यदि प्रत्येक सदिश अन्य दो सदिशो के योग पर लम्ब हो, तो सदिश →a+→b+→c का परिमाण ज्ञात किजिए।
03:32View Solutionयदि →a,→b,→c समान परिमाण के परस्पर लम्ब सदिश हो तो सिद्ध कीजिए कि सदिश →a+→b+→c सदिशों →a,→b और →c के साथ बराबर कोण बनाता है।
03:33View Solutionसदिश →a=ˆi+ˆj+ˆk का सदिशों →b=2ˆi+4ˆj−5ˆk तथा →c=λˆi+2ˆj+3ˆk के योगफल की दशा में एक मात्रक सदिश के साथ अदिश गुणनफल 1 के बराबर है का मान ज्ञात कीजिए तथा →b+→c की दशा में एक मात्रक सदिश ज्ञात कीजिए।
03:30View Solution→a और →b के मध्य कोण 5π6 है तथा →a तथा →b पर प्रक्षेप −9√3 है , तो |→a| है -
03:50View Solutionयदि →a=ˆi+2ˆj+2ˆk,∣∣→b∣∣=5 और →a तथा→b के बीच कोण π6 है , तब दोनों भुजाओं के रूप में इन दो सदिशों के द्वारा बनने वाले त्रिभुज का क्षेत्रफल है -
45:28View Solution

