The internal energy of one mole of a gas is
32RT
12kT
12RT
32kT
The correct Answer is:A
To determine the internal energy of one mole of a gas, we can follow these steps:
1. Understanding Internal Energy:
Internal energy (U) is a measure of the total energy contained within a system. For an ideal gas, the internal energy is primarily a function of temperature.
2. Using the Formula:
For one mole of an ideal gas, the internal energy can be expressed using the formula:
U=32nRT
where:
- U = internal energy
- n = number of moles (which is 1 in this case)
- R = universal gas constant (approximately 8.314J/(mol⋅K))
- T = absolute temperature in Kelvin
3. Substituting Values:
Since we are considering one mole of gas, we can substitute n=1:
U=32⋅1⋅RT=32RT
4. Conclusion:
Therefore, the internal energy of one mole of an ideal gas is given by:
U=32RT
Final Answer:
The internal energy of one mole of gas is 32RT.
---
Internal energy (U) is a measure of the total energy contained within a system. For an ideal gas, the internal energy is primarily a function of temperature.
For one mole of an ideal gas, the internal energy can be expressed using the formula:
U=32nRT
where:
- U = internal energy
- n = number of moles (which is 1 in this case)
- R = universal gas constant (approximately 8.314J/(mol⋅K))
- T = absolute temperature in Kelvin
Since we are considering one mole of gas, we can substitute n=1:
U=32⋅1⋅RT=32RT
Therefore, the internal energy of one mole of an ideal gas is given by:
U=32RT
The internal energy of one mole of gas is 32RT.
Topper's Solved these Questions
Similar Questions
An ideal gas is in thermodynamic equilibrium. The number of degrees of freedom of a molecule of the gas is n.The internal energy of one mole of the gas is Un and the speed of sound in the gas is vn.At a fixed temperature and pressure, which of the following is the correct option?
View SolutionCalculate the internal energy of one mole of a diatomic gas at 300 K. Assume the molecules to be rigid.
View Solution
Knowledge Check
- Question 1 - Select One
The internal energy of one mole of ideal gas is
A3/2RTB1/2kTC1/2RTD3/2kT - Question 2 - Select One
The internal energy of one mole of ideal gas is
A32RTB12KTC12RTD32KT - Question 3 - Select One
The molar specific heat of a gas at constant volume is 24 J/mol K. then change in its internal energy if one mole of such gas is heated at constant from 10∘C to 30∘C is
A240 JB480 JC360 JD720 J
Consider a P−V diagram in which the path followed by one mole of perfect gas in a cyclinderical container is shown in (figure)
(a) Find the work done when the gas is taken from state 1 to state 2.
(b) What is the ratio of temperatures T1/T2,ifV2=2V1?
(c ) Given the internal energy for one mole of gas at temperature Tis(3/2)RT, find the heat supplied to the gas when it is taken from state 1 to 2, with V2=2V1.
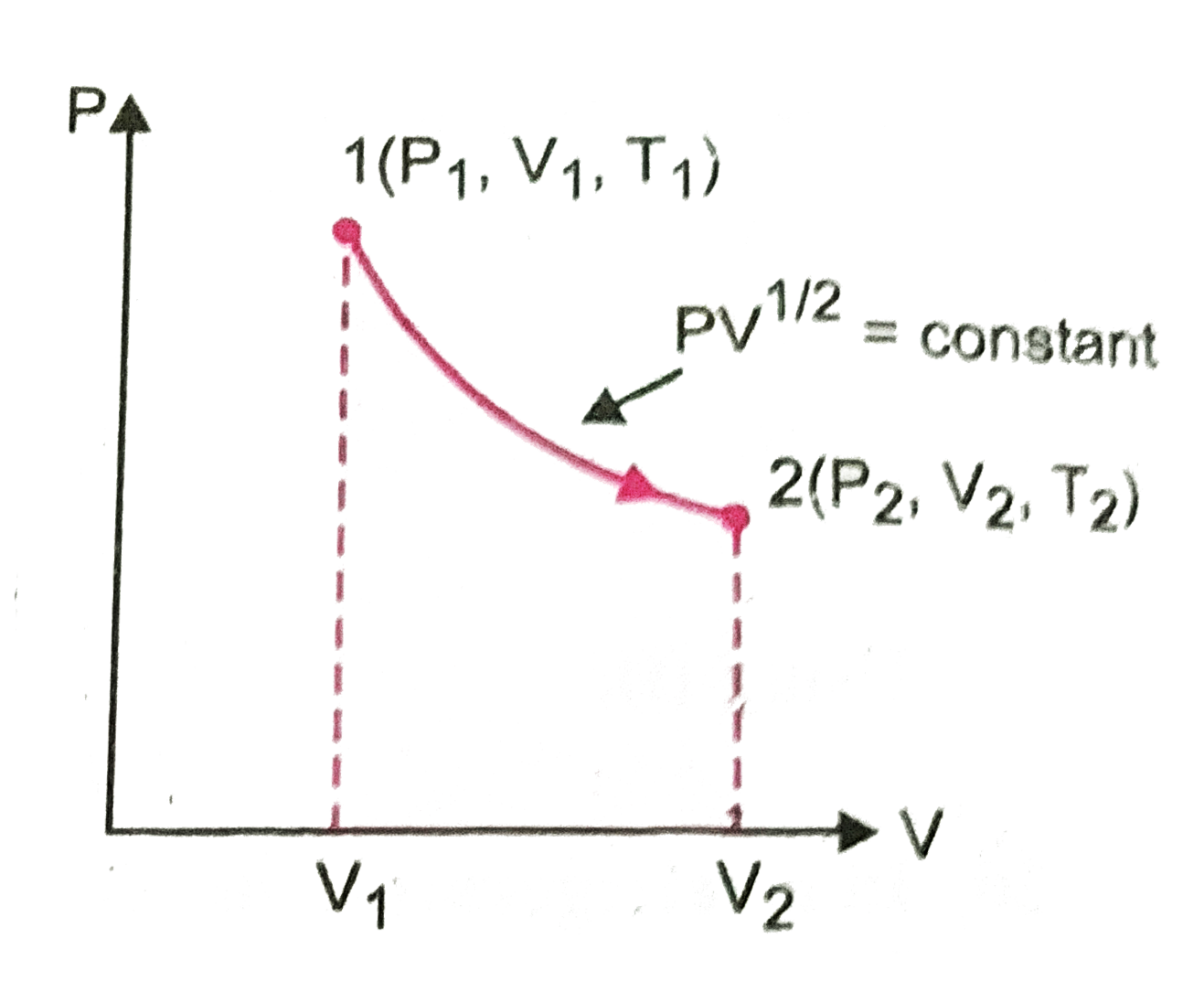 View Solution
View SolutionThe internal energy of one mole of the diatomic gas at 200 K is
View SolutionThe total internal energy of one mole of rigid diatomic gas is
View SolutionThe ratio of translational and rotational kinetic energies at 100K temperature is 3:2. Then the internal energy of one mole gas at that temperature is (R=8.3j/mol−K]
View SolutionThe change in internal energy of two moles of a gas during adiabatic expansion is found to be -100 Joule. The work done during the process is
View Solution

