The non- expansion work of a system
Equals decrease in free energy
Equals decrease in internal energy
Equals increase in enthalpy
Equals increase in internal energy
The correct Answer is:A
−ΔG=−Wnon−ecp
Topper's Solved these Questions
Similar Questions
Assertion lsothemal expansion of ideal gas againt vacuum must be simultaneously adiabatic.
reason The work done by system in the above process is zero.
View SolutionAmong the following,the state function(s) is/are. (A) Internal energy (B) Irreversible expansion work (C) Reversible expansion work (D) Molar enthalpy
View Solution
Knowledge Check
Which one of the following equations does not correctly represent the first law of thermodynamics for the given processes involving an ideal gas?
(Assume non-expansion work is zero)ACyclic process: q = -wBAdiabatic process: ΔU=−wCIspochoric process : ΔU=qDIsothermal process: q=−wFollowing graph shows a single stage expansion, then work done by the system is:
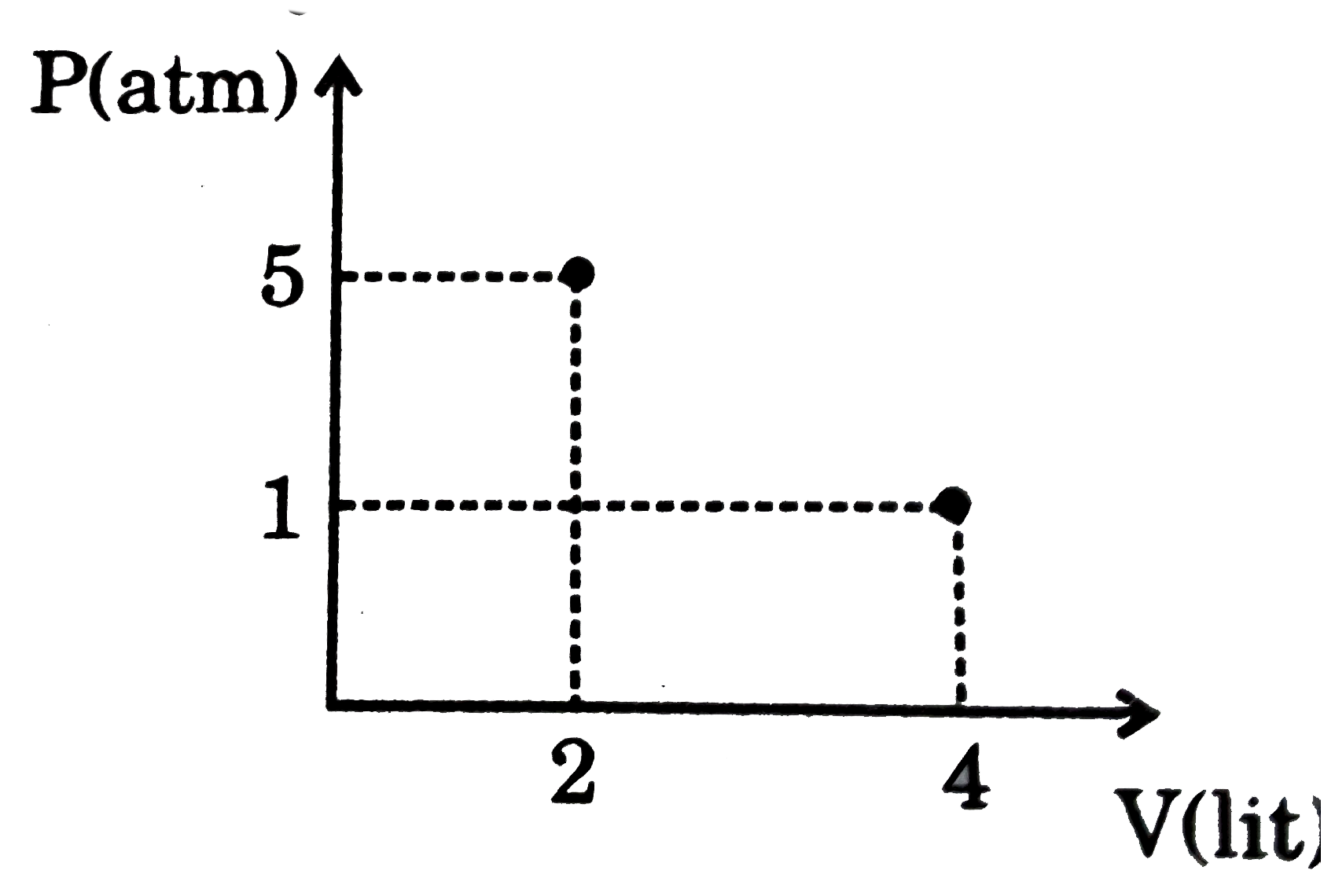A−9104JB−202.6JC−506JD−101.3JSelect the correct set of statement/s :
(P) Work done by the surroundings in case of infinite stage expansion is more than single stage expansion.
(Q) Irreversible work is always greater than reversible work.
(R ) In an ideal gas in case of single stage expansion and compression, system as well as surroundings are restored back to their orginal states.
(S) If gas in thermodynamics is equilibrium is taken from state A to state B, by four successive single stage expansion. Then we can plot four points on the P−V indicator diagram.AOnly QBP,Q,R,SCQ,SDP,Q,S
(a) Write any six thermodynamic state functions
(b) Reversible isothermal expansion work formula.
(c ) Irreversible isothermal expansion work formula.
View Solutionif work is done by the system then W is
View SolutionA solid with coefficient of linear expansion aplha just floats in a liquid whose coefficient of volume expansion is γ . If the system is heated, the solid will
View SolutionThe work done in an isothermal reversible expansion of n moles of a gas is
View SolutionThe work done during expansion of a gas in vacuum is zero, because there is
View Solution