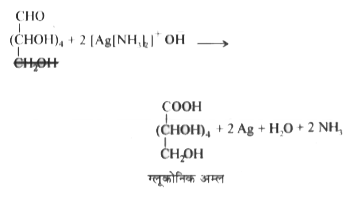
सिद्ध कीजिए कि D-ग्लूकोस एक अपचायी शर्करा है।
D-ग्लूकोस फेहलिंग विलयन तथा टॉलेन अभिकर्मक को अपचयित कर देता है, अत: यह एक अपचायी शर्करा है। ग्लूकोस की टॉलेन अभिकर्मक के साथ अभिक्रिया निम्न प्रकार होती है-
Topper's Solved these Questions
- जैव-अणुBOOK - SANJEEV PUBLICATIONCHAPTER - जैव-अणुEXERCISE - निबन्धात्मक प्रश्न
2 Videos
- जैव-अणुBOOK - SANJEEV PUBLICATIONCHAPTER - जैव-अणुEXERCISE - पाठ्यपुस्तक के अभ्यास प्रश्न (निबन्धात्मक प्रश्न)
10 Videos
- उपसहसंयोजक यौगिक BOOK - SANJEEV PUBLICATIONCHAPTER - उपसहसंयोजक यौगिक EXERCISE - अन्य महत्वपूर्ण प्रश्न लघुत्तरात्मक प्रश्न
90 Videos
- ठोस अवस्थाBOOK - SANJEEV PUBLICATIONCHAPTER - ठोस अवस्थाEXERCISE - अन्य महत्तवपूर्ण प्रश्न ( निबन्धात्मक प्रश्न )
9 Videos
Similar Questions
कार्बोहाइड्रेटों का वर्गीकरण कीजिए तथा प्रत्येक के उदाहरण भी दीजिए।
View Solutionसेलूलोस तथा स्टार्च के मुख्य ग्रोत क्या हैं।
View Solutionसंयोजकता बंध सिद्धांत के आधार पर संकुल [CoF6]3− कि ऑक्सीकरण अवस्था, संकरण, ज्यामिति एवं चुंबकीय प्रकृति को समझाइये।
View Solutionसोडियम (Na) की कायकेन्द्रित घनीय (BCC) संरचना होती है तो 2 ग्राम सोडियम में एकक कोष्ठिकाओं की संख्या ज्ञात कीजिए। (Na का परमाणु द्रव्यमान =23)
View Solutionसिद्ध कीजिए कि समीकरण y2+2ax+2by+c=0 एक परवलय निरूपित करती है जिसका अक्ष x-अक्ष के समान्तर है । इसका शीर्ष ज्ञात कीजिए ।
View Solutionसिद्ध कीजिए कि बिंदु (1,−6),(5,2),(7,0) तथा (−1,−4)एक चक्रीय चतर्भुज के शीर्ष है ।
View Solutionमाना कि N में एक द्वि - आधारी संकिया ∗, a∗b=a तथा b के LCM द्वारा परिभाषित है , a,b∈N तब सिद्ध कीजिए कि :(20∗16)∗8=20∗(16∗8)
View Solutionसिद्ध कीजिए कि निम्नलिखित संख्याएँ अपरिमेय संख्याएँ है-
32√5
View Solutionएक ही आधार BC पर तीन समद्विबाहु त्रिभुज △PBC ,△QBC और △RBC स्तिथ है। सिद्ध कीजिए कि P ,Q और R समरेख है।
View SolutionABCDE एक समपंचभुज है। O इसका केंद्र है। सिद्ध कीजिए कि −−→OA+−−→OB+−−→OC+−−→OD+−−→OE=→0
View Solutionसिद्ध कीजिए कि बिन्दु (2,−2),(8,4),(5,7) और (−1,1) एक आयत के शीर्ष है। उसके विकर्णों के बीच का न्यून कोण ज्ञात कीजिए।
View Solutionयदि f:R→R इस प्रकार है कि f(x) = |x|, तो सिद्ध कीजिए कि fof = f .
View Solutionसिद्ध कीजिए कि f(x)=ax,o<a<1,R में ह्रासमान है।
View Solutionसिद्ध कीजिए कि [→a×→b→a×→c→d]=[→a.→d][→a→b→c]
View Solutionयदि →a×→b=→c×→bतो सिद्ध कीजिए →a−→c=λ→b कि जहाँ एक λ अदिश है।
View Solutionयदि ∣∣→a+→b∣∣=∣∣→b∣∣, तो सिद्ध कीजिए कि →a और →a+2→b परस्पर लम्ब है।
View Solution
