Which of the following represents the expression for th life of first order reaction?
The correct Answer is:C
To find the expression for the 34th life of a first-order reaction, we can follow these steps:
Step 1: Understand the first-order reaction kinetics
The rate of a first-order reaction can be described by the equation:
\( T = \frac{2.303}{k} \log \frac{A}{A - x} \)
where:
- \( T \) is the time taken for the concentration to change from \( A \) to \( A - x \),
- \( k \) is the rate constant,
- \( A \) is the initial concentration,
- \( x \) is the amount reacted.
Step 2: Determine the value of \( x \) for 34th life
For 34th life of the reaction, we need to find the time taken for the concentration to decrease from \( A \) to \( A - x \) where \( x = \frac{3}{4}A \). This means that \( 3/4 \) of the initial concentration has reacted.
Step 3: Calculate \( A - x \)
Substituting \( x \) into the equation:
\( A - x = A - \frac{3}{4}A = \frac{1}{4}A \)
Step 4: Substitute into the first-order rate equation
Now, we can substitute \( A \) and \( A - x \) into the first-order reaction equation:
\( T = \frac{2.303}{k} \log \frac{A}{A - x} = \frac{2.303}{k} \log \frac{A}{\frac{1}{4}A} \)
Step 5: Simplify the logarithm
This simplifies to:
\( T = \frac{2.303}{k} \log \frac{A}{\frac{1}{4}A} = \frac{2.303}{k} \log 4 \)
Conclusion
Thus, the expression for the 34th life of a first-order reaction is:
\( T = \frac{2.303}{k} \log 4 \)
Final Answer
The correct option representing the 34th life of a first-order reaction is:
\( \frac{2.303}{k} \log 4 \)
---
The rate of a first-order reaction can be described by the equation:
\( T = \frac{2.303}{k} \log \frac{A}{A - x} \)
where:
- \( T \) is the time taken for the concentration to change from \( A \) to \( A - x \),
- \( k \) is the rate constant,
- \( A \) is the initial concentration,
- \( x \) is the amount reacted.
For 34th life of the reaction, we need to find the time taken for the concentration to decrease from \( A \) to \( A - x \) where \( x = \frac{3}{4}A \). This means that \( 3/4 \) of the initial concentration has reacted.
Substituting \( x \) into the equation:
\( A - x = A - \frac{3}{4}A = \frac{1}{4}A \)
Now, we can substitute \( A \) and \( A - x \) into the first-order reaction equation:
\( T = \frac{2.303}{k} \log \frac{A}{A - x} = \frac{2.303}{k} \log \frac{A}{\frac{1}{4}A} \)
This simplifies to:
\( T = \frac{2.303}{k} \log \frac{A}{\frac{1}{4}A} = \frac{2.303}{k} \log 4 \)
Thus, the expression for the 34th life of a first-order reaction is:
\( T = \frac{2.303}{k} \log 4 \)
The correct option representing the 34th life of a first-order reaction is:
\( \frac{2.303}{k} \log 4 \)
Topper's Solved these Questions
- CHEMICAL KINETICSBook:DINESH PUBLICATIONChapter:CHEMICAL KINETICSExercise:Comprehension type
Explore 14 Videos
- CHEMICAL KINETICSBook:DINESH PUBLICATIONChapter:CHEMICAL KINETICSExercise:Stright objective types MCQs
Explore 24 Videos
- CHEMICAL KINETICSBook:DINESH PUBLICATIONChapter:CHEMICAL KINETICSExercise:Effect of temperature and catalyst on rate of reaction.
Explore 15 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBook:DINESH PUBLICATIONChapter:CHEMICAL BONDING AND MOLECULAR STRUCTUREExercise:Unit Test - 1
Explore 20 Videos
- CHEMICAL THERMODYNAMICS AND CHEMICAL ENERGETICS Book:DINESH PUBLICATIONChapter:CHEMICAL THERMODYNAMICS AND CHEMICAL ENERGETICS Exercise:Exercise
Explore 507 Videos
Similar Questions
Knowledge Check
Which of the following represents the expression for 3/4th life of a first order reaction?
Ak2.303log4/3B2.303klog3/4C2.303klog4D2.303klog3Which of the following represent the expression for 34th life of first order reaction
Ak2.303log4/3B2.303klog3/4C2.303klog4D2.303klog3Which of the following represents zero order reaction ?
A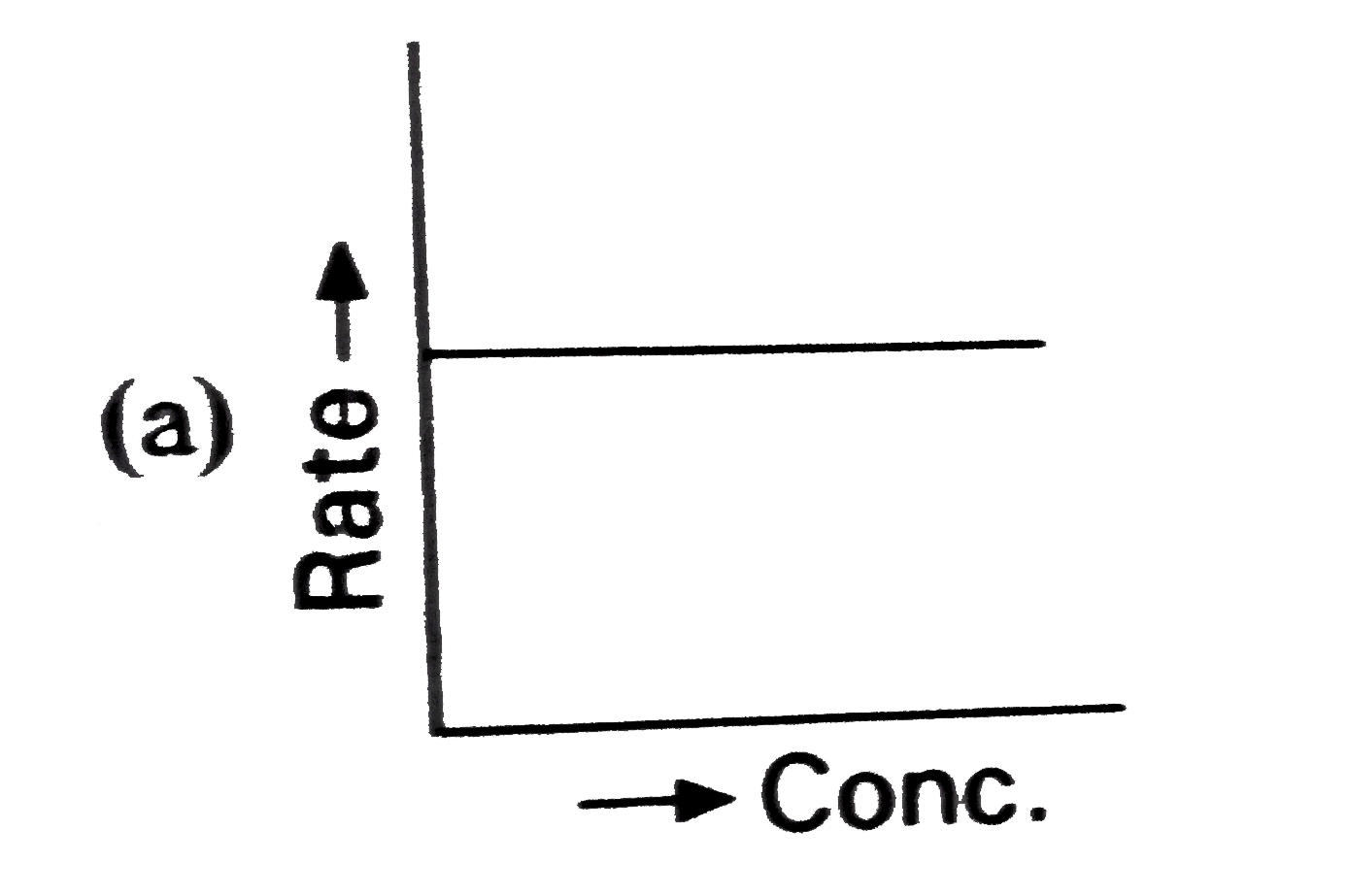 B
B C
C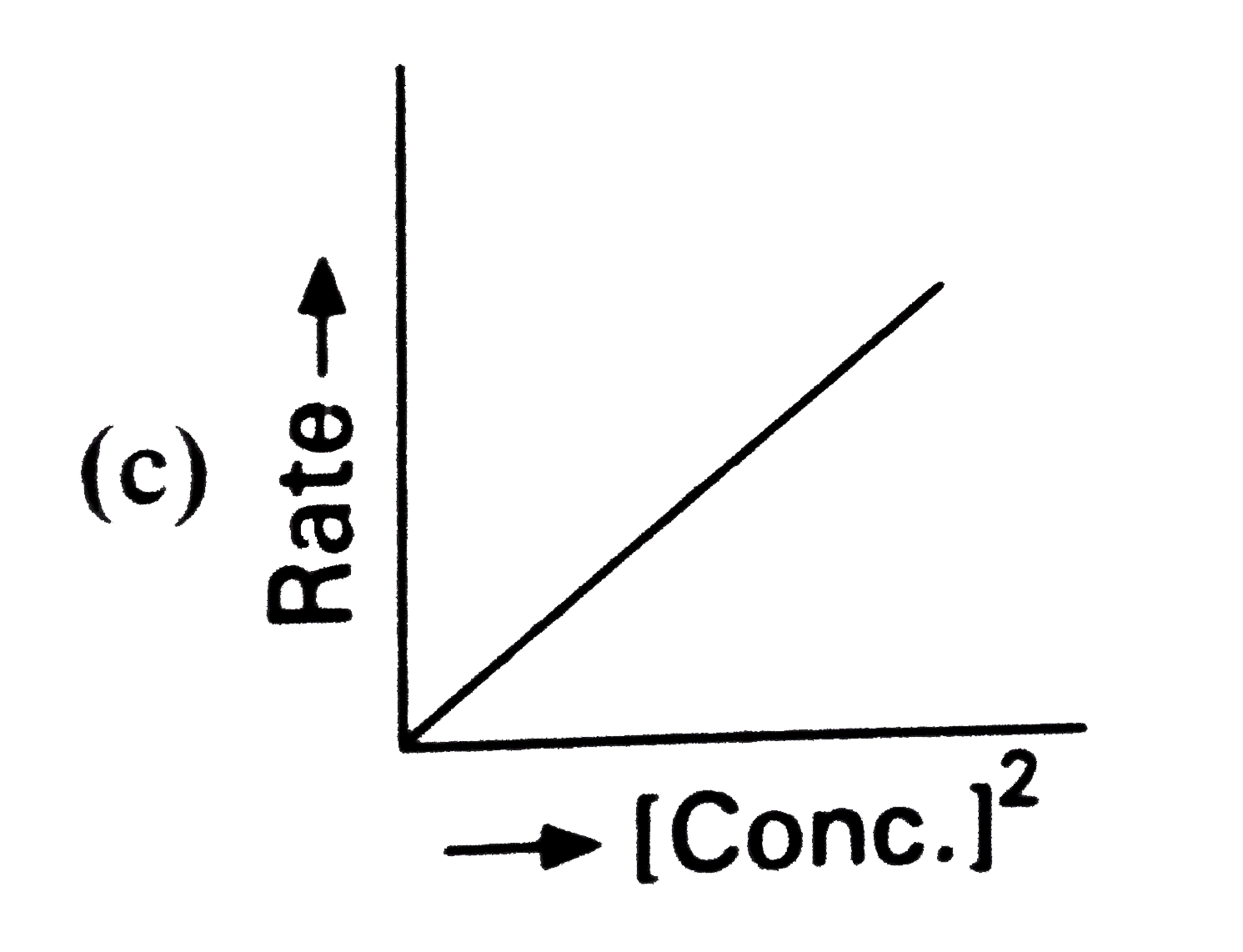 D
D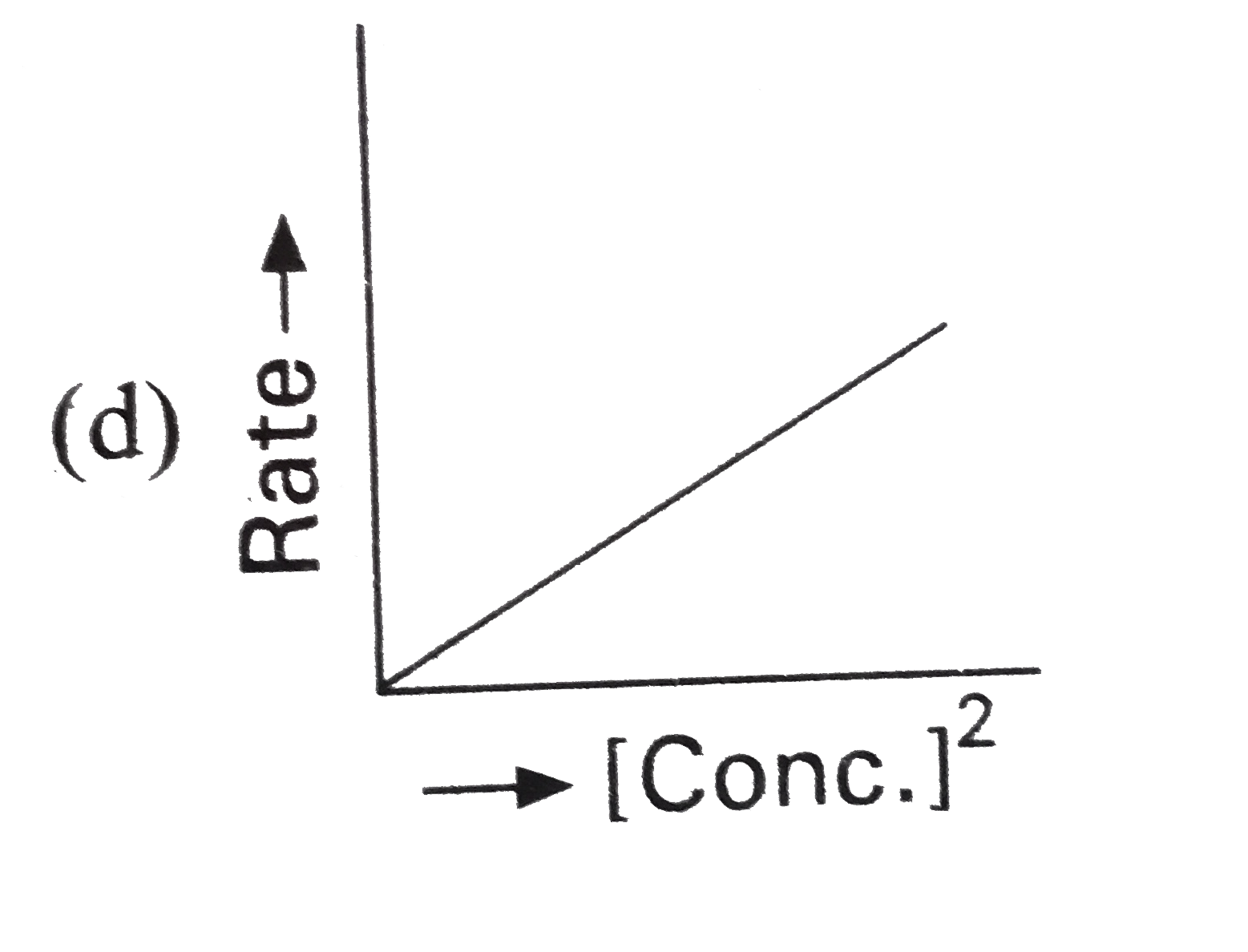
For which of the following represents the expresison for theee/fourth life reaction?
View SolutionWhich of the following is a first order reaction ?
View SolutionWhich of the following is a first order reaction ?
View SolutionExpression for the half-life of zero order reaction is given as
View SolutionWhich of the following is a first order reaction:
View Solution