The activation energy for a reaction at the temperature T K was found to be 2.303RTJmol−1. The ratio of the rate constant to Arrhenius factor is
10−1
10−2
2×10−3
2×10−2
The correct Answer is:A
a) According to Arrhenius equation,
log k = log A−E2.303R×1T
2.303logk=2.303logA−EaRT
Substituting the value of Ea as 2.303 RT and dividing by 2.303 on both sides, we get.
log k−logA=−1
log(kA)=log10−1
Taking anti log.
(kA)=10−1
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - Comprehension type
14 Videos
- CHEMICAL KINETICSBOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - Stright objective types MCQs
24 Videos
- CHEMICAL KINETICSBOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL KINETICSEXERCISE - Effect of temperature and catalyst on rate of reaction.
15 Videos
- CHEMICAL BONDING AND MOLECULAR STRUCTUREBOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - Unit Test - 1
20 Videos
- CHEMICAL THERMODYNAMICS AND CHEMICAL ENERGETICS BOOK - DINESH PUBLICATIONCHAPTER - CHEMICAL THERMODYNAMICS AND CHEMICAL ENERGETICS EXERCISE - Exercise
507 Videos
Similar Questions
Consider the following reversible reaction, AgBg→ABg . The activation energy of the backward reaction exceeds that of the forward reaction by 2(∈Jmol1). If the pre-exponential factor of the forward reaction is 4 times that of the reverse reaction, the absolute value of△Gθ(∈Jmol−1) for the reaction at 300 K is ____. (Given, ln(2) = 0.7,=2500Jmol−1 at 300 K and G is the Gibbs energy)
View SolutionConsider the following reversible reaction :
A(g)+B(g)⇔AB(g).
The activation energy of the backward reaction exceeds that of the forward reaction by 2RT (in J mol−1). If the pre-exponential factor of the forward reaction is four times that of the reverse reaction, the absolute value of △G∘(in J mol−1) for the reaction at 300K is...... (Given ln 2=0.7, RT=2500 J mol−1 at 300K and G is the Gibbs energy)
View Solution
Knowledge Check
The activation energy for a reaction at temperature T K was found to be 2.303 RT J mol−1. The ratio of the rate constant to Arrhenius factor is
A10−1B10−2C2×10−3D2×10−2The activation energy for a reaction at temperature T K was found to be 2.303 RT J mol−1. The ratio of the rate constant to Arrhenius factor is
A10−1B10−2C2×10−3D2×10−2The activation energy for a reaction at temperature T K was found to be or 2.303RT J mol−1. The ratio of the rate constant to Arrhenius factor is
A10−1B10−2C2×10−3D2×10−2
The activation energy of a reaction at a given temperature is found to be 2.303 RT J mol−1. The ratio of rate constant to the Arrhenius factor is
View SolutionThe activation energy of a reaction is 58.3 kJ mol−1. The ratio of rate constants at 305 K and 300 K is about (R= 8.3 J K−1mol−1)
View SolutionAccording to collision theory for determining the variation of rate of reaction with temperature the rate constant,k=Ae−Ea/RT. For most of the practical purposes A and Ea[Arrhenius factor and Activation energy] are temperature independent. However they may vary slightly.
Assuming the conditions given above answer the following questions.
IfA=K,TandEa=K2T2 and the given equation is still applicable where K1andK2 are the constant and T represent temperature then which will be correct option?
(P) The maximum value of k will be equal to A
(Q) At lower temperature rate of reaction will increase with increase in temperature
(R) At higher temperature, rate of reaction will decrease with increase in temperature
View SolutionThe rate constant , the activation energy and Arrhenius parameter of a chemical reaction at 25∘C are x, 10x kJ/ mol and 2xs−1 . Value of rate constant as T→∞ is
View SolutionWhen the temperature is increased, heat is supplied which increases the kinetic energy of the reacting molecules. This shall increase the number of collisions and ultimately the rate of reaction shall be enhanced. Arrhenius suggested a equation which describes K as a function of temperature, i.e.
k=Ae−Ea/RT
where
k= rate constant
A= a constant (frequency factor)
Ea= energy of activation
log10k=log10A−Ea2.303R[1R]
Y=C+MX
It is the equation of straight line with negative slope. On plotting log10k against [1T] we get a straight line as shown below :
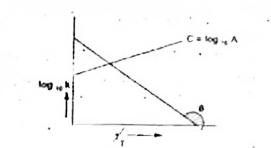
The slope gives activation energy and intercept gives frequency factor.
Also log.k2k1=Ea2.303[T2−T1T1T2]
The rate of certain reaction increases by 2.5 times when the temperature is raised from 300K to 310K. If k is the rate constant at 300K then rate constant at 310K will be equal to
View Solution
