The number of geometrical isomers that can exist for the square planar complex is :
A
4
B
6
C
2
D
3
Text Solution
The correct Answer is:D
The complex is also MABCD type and is the square planar in nature. Three geometrical isomers also possible.

|
Topper's Solved these Questions
- CO-ORDINATION COMPOUNDS BOOK - DINESH PUBLICATIONCHAPTER - CO-ORDINATION COMPOUNDS EXERCISE - Comprehension types
19 Videos
- CO-ORDINATION COMPOUNDS BOOK - DINESH PUBLICATIONCHAPTER - CO-ORDINATION COMPOUNDS EXERCISE - Straight objective type mcqs
17 Videos
- CO-ORDINATION COMPOUNDS BOOK - DINESH PUBLICATIONCHAPTER - CO-ORDINATION COMPOUNDS EXERCISE - Assignment
76 Videos
- CHEMISTRY IN EVERY DAY LIFEBOOK - DINESH PUBLICATIONCHAPTER - CHEMISTRY IN EVERY DAY LIFEEXERCISE - Unit test-9
50 Videos
- CYANIDES, ISOCYANIDES, NITROCOMPOUNDS AND AMINESBOOK - DINESH PUBLICATIONCHAPTER - CYANIDES, ISOCYANIDES, NITROCOMPOUNDS AND AMINESEXERCISE - Unit test - 8
20 Videos
Similar Questions
Knowledge Check
The number of geometric isomers that can exist for square planner complex ion [Pt(CI)(PY)(NH3)(NH2OH)]+ is (Py = pyridine) :
A4B6C2D3The number of geometric isomers that can exist for square planner complex ion [Pt(CI)(PY)(NH3)(NH2OH)]+ is (Py = pyridine) :
A3B4C6D2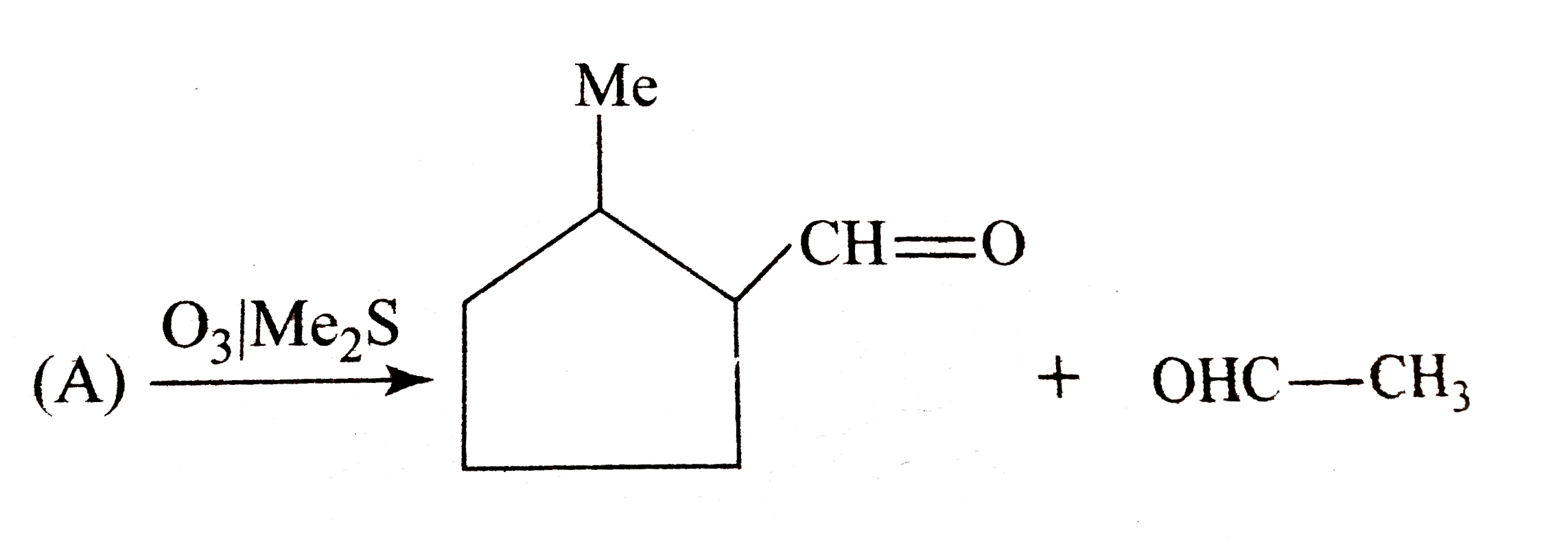
The number of geometrical isomers of (A) can be :A2B3C4D5
The number of geometric isomers that can exist for square planar [Pt(C1)(py)(NH3)(NH2OH)+] is (py = pyridine).
View SolutionGeometrical isomers can exists for :
View SolutionGeometrical isomers can exists for :
View SolutionThe number of geometric isomers that can exist for square planar [Pt(C1)(py)(NH3)(NH2OH)+] is (py = pyridine).
View SolutionThe number of geometric isomers that can exist for square planar [Pt(C1)(py)(NH3)(NH2OH)+] is (py = pyridine).
View Solution
