दो नक्षत्रों के केंद्रों के बीच की दूरी 10a है। इन नक्षत्रों के द्रव्यमान M तथा 16 M और त्रिज्याएँ क्रमश: a तथा 2a हैं। m द्रव्यमान का एक पिण्ड बड़े नक्षत्र के पृष्ठ से सीधा छोटे नक्षत्र की ओर दागा जाता है। इस पिण्ड की न्यूनतम प्रारम्भिक चाल, जिससे कि यह छोटे नक्षत्र के पृष्ठ तक पहुँच जाये, G, M तथा a के पदों में ज्ञात कीजिए।
The correct Answer is:
माना दो नक्षत्र (1) व (2) है जो चित्र में दर्शाए गए हैं।
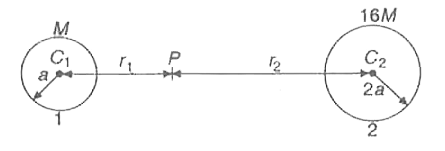
माना व के बीच कोई बिंदु P है जहाँ गुरुत्वीय क्षेत्र शून्य है अर्थात P पर नक्षत्र (1) के कारण तीव्रता, नक्षत्र (2) के कारण तीव्रता के बराबर तथा विपरीत है।
अत:
या तथा
तथा
अब, m द्रव्यमान का एक पिण्ड बड़े नक्षत्र से छोटे नक्षत्र की ओर प्रेक्षेपित किया जाता है। तथा P के बीच यह पिण्ड नक्षत्र (2) की ओर आकर्षित होगा तथा व P के बीच यह नक्षत्र (1) की ओर आकर्षित होगा। इस प्रकार पिण्ड केवल P तक पहुँचने के लिए प्रेक्षेपित की जानी चाहिए क्योंकि उसके पश्चात वह स्व्यं ही छोटे नक्षत्र की ओर आकर्षित हो जायेगा। यांत्रिक ऊर्जा संरक्षण के नियम से
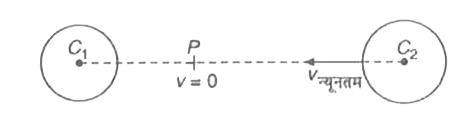
पर पिण्ड की स्थितिज ऊर्जा – बड़े तारे की सतह पर स्थितिज ऊर्जा
या
Topper's Solved these Questions
- गुरुत्वाकर्षण BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - गुरुत्वाकर्षण EXERCISE - एकल पूर्णांक उत्तर प्रकार
4 Videos
- गति के नियम BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - गति के नियम EXERCISE - श्रृंखलाबद्ध -बोधन प्रकार
2 Videos
- घूर्णन गतिBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - घूर्णन गतिEXERCISE - श्रृंखलाबद्ध बोधन प्रकार
10 Videos
Similar Questions
एक युग्मतारे में दो तारे A (द्रव्यमान 2.2 Ms) तथा B (द्रव्यमान 11Ms) है, Ms सूर्य का द्रव्यमान है। यह तारे d दूरी पर हैं तथा अपने संहति केंद्र, जो कि स्थिर है, के चारों ओर घूम रहें हैं। युग्म तारे के कुल कोणीय संवेग तथा B तारे के, संहति केंद्र के सापेक्ष, कोणीय संवेग का अनुपात है।
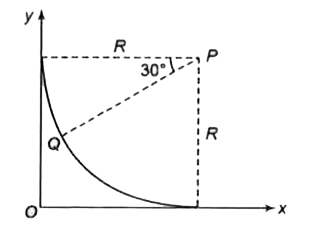
View Solutionएक रुक्ष पृथ के उच्चतम बिन्दु से 1 किग्रा द्रव्यमान के गुटके को विरामावस्था से छोडा जाता है। यह पथ 40 मी त्रिज्या का वृत्तीय चाप है। गुटका अपने पथ पर बिना लड़के हुए सरकता है। इस गुटके पर एक घर्षण बल तात्क्षणिक वेग की विपरीत दिशा में लगता है। चित्र में दर्शाए गए अनुसार , बिन्दु O तक आने के लिए घर्षण को अतिक्रम करने के लिए 150 जूल कार्य करना पड़ा है। (गुरुत्वीय त्वरण g=10मी/से2 लीजिए)
 .
.
जब गुटका बिन्दु Q पर पहुँचता है , इसकी गति है
View Solutionदो डिस्कें A तथा B एक ऊर्ध्वाधर धुरी पर समाक्ष रूप से अवस्थिरत की गई है। उभयनिष्ठ अक्ष के परितः उन चकतियों के जड़त्व आघूर्ण क्रमशः I तथा 2I है। एक स्पि्रंग को x1 दूरी से दबाकर उसकी सम्पूर्ण स्थितिज ऊर्जा का उपयोग करके, चकती A को प्रारंभिक कोणीय वेग 2ω दिया जाता है। उतने ही स्पि्रंग गुणांक वाले एक दूसरे स्पि्रंग को x2 दूरी से दबाकर डिस्क B को कोणीय वेग ω दिया जाता है। दोनों चकतियां दक्षिणावर्त दिशा में घूम रही हैं
अनुपात x1/x2 है।
View Solutionकिसी समबाहु त्रिभुज के आधार का समीकरण x+y=2 है तथा सामने के शीर्ष के निर्देशांक (2,1) है , त्रिभुज की शेष भुजाओ के समीकरण ज्ञात कीजिए ।
View Solutionएक व्यक्ति के एक कदम आगे चलने की प्रायिकता 0.4 तथा एक कदम पीछे हटने की प्रायिकता 0.6 है। प्रायिकता ज्ञात कीजिए कि 5 कदम चलने के पश्चात, यह व्यक्ति प्रारम्भिक बिन्दु से एक कदम दूर है।
View Solutionयदि एक अतिपरवलय के संयुग्मी अक्ष की लम्बाई 5 है तथा इसकी नाभिको के बीच की दुरी 13 है, तो इस अतिपरवलय की उत्केंद्रता है
View Solutionएक शतरंज प्रतियोगिता में m पुरुष तथा दो महिलाएं भाग ले रही है । प्रत्येक प्रतिभागी (participant) दूसरे प्रत्येक प्रतिभागी के साथ दो गेम खेलता है । यदि पुरुषो के बीच आपस में खेले गए गेमों कि संख्या, पुरुष तथा महिलाओ के बीच खेले गए गेमों की संख्या से 84 अधिक है , तो m का मान है
View Solutionएक वस्तु जिसका द्रव्यमान m है विराम से h ऊँचाई से गुरुत्वीय त्वरण g के अन्तर्गत गिरती है तथा यह रेत में गहराई d तक धंसती है। रेत में फँसने के दौरान औसत मन्दन होगा
View Solutionबिंदुओं (3,1) और (0,y) के बीच की दूरी 5 है। y ज्ञात कीजिए।
View Solutionएक बिंदु की एक रेखा से दूरी|दो समान्तर रेखाओं के बीच की दूरी
View Solutionसूर्य और पृथ्वी के बीच की दूरी 1.496×108 km है तथा पृथ्वी और चंद्रमा के बीच की दूरी 3.84×108m है सूर्य ग्रहण होने पर चन्द्रमा पृथ्वी और सूर्य के बीच में आ जाता है इस विशेष समय पर सूर्य और चंद्रमा के बीच की दूरी क्या है ?
View Solutionसमान्तर रेखाओं ax+by+c=0 तथा ax+by+d=0 के बीच की दुरी निकालें।
View Solutionजल के अणु के विलोपन के साथ ऐल्कोहॉल और एक अम्ल के बीच की अभिक्रिया को कहा जाता है
View Solution1.0 mg के द्रव्यमान वाले एक कण का वेग 3600 km/h है। कण के तरंग दैर्ध्य की गणना कीजिए।
View Solutionसल्फर के एक यौगिक में द्रव्यमान द्वारा 8% सल्फर उपस्थित होता है। यौगिक के न्यूनतम आण्विक द्रव्यमान की गणना कीजिए।
View Solutionकॉपर सल्फेट के साथ धातु हाइड्रॉक्साइड (MOH) और समान वर्ग की अन्य धातु M_1 के साथ धातु M के मिश्रित टार्टेट के विलयन का उपयोग -CHO समूह की पहचान में किया जाता है। धातु M और M_1 क्रमश: हैं:
View Solution
