एक ठोस पिण्ड X जिसकी उष्माधारिता C है, ताप केल्विन पर वायुमण्डल में रखा गया है | समय t = 0 पर X का ताप केल्विन है | यह न्यूटन के शीतलन नियम के अनुसार ठंडा होता है | समय पर इसका ताप 350 केल्विन पाया जाता है | इस समय पर पिण्ड X को एक चालक-छड़ के द्वारा वायुमणडल ताप पर एक बड़े बक्से Y से जोड़ दिया जाता है | चालक-छड़ की लम्बाई L परिच्छेद क्षेत्रफल A तथा ऊष्मा छलकता K है | Y की उष्माधारिता इतनी अधिक है कि इसके ताप में होने वाले परिवर्तन को नगण्य माना जा सकता है | जोड़ी जाने वाली छड़ का परिच्छेद क्षेत्रफल A पिण्ड X के पृष्ठ क्षेत्रफल की तुलना में बहुत कम है | समय पर पिण्ड X का ताप ज्ञात कीजिए |
The correct Answer is: केल्विन
प्रश्न के प्रथम भाग में
पर, केल्विन तथा पर केल्विन
वातावरण का ताप, केल्विन (नियतांक)
न्यूटन के शीतलन के नियम के अनुसार यह शीतल हो जाएगा |
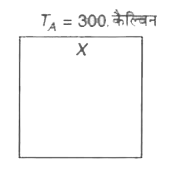
शीतलन की दर तापान्तर
या
या
या
या ....(i)
दूसरे भाग में , पिण्ड X विकिरण (Radiation) तथा चालन (Convection) द्वारा शीतलता प्रवाह करता है (न्यूटन के नियमानुसार)
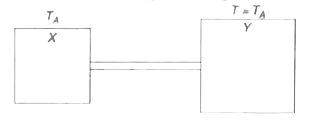
शीतलन की दर = विकिरण द्वारा शीतलन + चालन द्वारा शीतलन
...(ii)
चालन में,
जहाँ, C = X की उष्माधारिता
....(iii)
माना , पर X का ताप है |
समी (iii) से,
या
या
हल करने पर, केल्विन
Topper's Solved these Questions
- ऊष्मा एवं उष्मागतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - ऊष्मा एवं उष्मागतिकी EXERCISE - श्रृंखलाबद्ध - बोधन प्रकार
5 Videos
- ऊष्मा एवं उष्मागतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - ऊष्मा एवं उष्मागतिकी EXERCISE - एकल पूर्णांक उत्तर प्रकार
7 Videos
- MOCK TEST 2022BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - MOCK TEST 2022EXERCISE - प्रश्न
18 Videos
- कार्य ऊर्जा एव सामर्थ्य BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - कार्य ऊर्जा एव सामर्थ्य EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार
6 Videos
Similar Questions
ऊष्मा के चालक पदार्थ से बने तथा स्थिर रखे गए बेलन की त्रिज्या R तथा ऊँचाई L0 है | बेलन नीचे से खुला है तथा इसके ऊपरी सिरे में एक छोटा छेद है, जैसा कि चित्र में दिखाया गया है | एक पिस्टन जिसका द्रव्यमान M है, ऊपरी सतह से L दुरी पर पकड़ा हुआ है | वायुमण्डलीय दाब P0 है |
अब पिस्टन को बाहर की ओर धीरे - धीरे खिंचा जाता है तथा ऊपर से 2L दूरी पर पकड़ कर रखा जाता है, तब बेलन में ऊपरी सिरे तथा पिस्टन के बीच के भाग में दाब होगा |

View Solutionधातु की 10x लम्बाई वाली छड़ AB की छोर A0∘C पर रखी बर्फ में तथा दूसरा छोर B100∘C पर रखे पानी में रखा गया है | इस छड़ के एक अन्य बिन्दु P को 400∘C के स्थिर तापमान पर रखा जाता है कि A छोर पर प्रति इकाई समय में पिघलने वाली बर्फ का द्रव्यमान तथा B छोर पर प्रति इकाई समय में वाष्पित होने वाले जल का द्रव्यमान बराबर है | पानी के वाष्पीकरण तथा बर्फ के पिघलने की गुप्त ऊष्माएँ क्रमशः 540 कैलोरी ग्राम−1 तथा 80 कैलोरी ग्राम−1 है | यदि P की दुरी बर्फ वाले छोर से λx हो, तो λ का मान निकालें | (वातावरण में होने वाली ऊष्मा हानि को नगण्य मानें |)
View Solutionमान लीजिये मुक्त आकाश (free space) में एक गोलाकार गैस के बादल का द्रव्यमान घनत्व ρ(r) है तथा इसकी केन्द्र से त्रिज्य (radial) दूरी r है I यह गैसीय बादल m द्रव्यमान के समान कणों से बना है जो कि एक समकेंद्रीय वृत्ताकार कक्षाओं में समान गतिज ऊर्जा K से घूम रहे हैं। इन कणों पर पारस्परिक गुरुत्वाकर्षण बल लग रहा है। यदि ρ(r) समय के साथ एक स्थिर राशि है, तब कणों का संख्या घनत्व n(r) = ρ(r)/m का मान होगा,
[G सार्वत्रिक गुरुत्वीय नियतांक है]
View Solutionएक नत समतल के घर्षण रहित पृष्ठ पर M द्रव्यमान का एक छोटा गुटका गतिमान है, बिंदु B पर नत समतल का कोण 60∘से 30∘ अचानक परिवर्तित होता है। गुटका प्रारम्भ में बिंदु A पर विरामावस्था में है। नत समतल तथा गुटके के बिच संघट्ट अप्रत्यास्थ माना गया (g=10मीसे2)
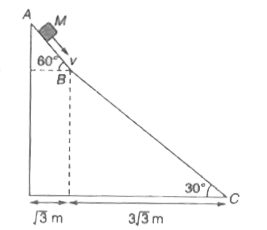
दूसरे नत समतल से टकराने के तुरंत बाद बिंदु B पर गुटके की चाल है
View Solutionअभिक्रिया के वेग पर ताप का प्रभाव
View Solutionआयोडीन एक ठोस है और साधारण ताप पर ऊर्ध्वपातित होता है। इसका कारण है:
View Solutionविभिन्न ताप पर अधिशोषण की सीमा (x//m) बनाम दाब का आरेख इस प्रकार है : वक्रो I ,II ,III ,IV के लिए बढ़ते ताप का सही क्रम है :
View Solutionकिस ताप (केल्विन में) पर हाइड्रोजन अणुओं की वर्ग माध्य मूल चाल, 1327∘C पर ऑक्सीजन अणुओं के समान है?
View Solutionएक आरेख को अलग-अलग ताप पर, दाब और आयतन के मध्य आलेखित किया जाता है। आरेख के आधार पर आप किन परिवर्तनों का प्रेक्षण करेंगे, यदि (i) नियत ताप पर, दाब बढ़ता है (ii) नियत दाब पर, ताप घटता है
View Solutionएक निश्चित ताप पर N2O4 का वाष्प घनत्व 30 है। इस ताप पर N2O4 का प्रतिशत वियोजन क्या है?
View Solutionजब एक निश्चित ताप पर 3c-2e के साथ-साथ 2c 2e बंध वाला एक अकार्बनिक यौगिक (X), अमोनिया गैस के साथ अभिक्रिया करता है, तो बेन्जीन के समान संरचना वाले यौगिक (Y) का निर्माण होता है। उच्च ताप पर यौगिक (X), अमोनिया के साथ एक पदार्थ (Z) का उत्पादन करता है। निम्न में से कौनसा विकल्प सही नहीं है?
View SolutionX' निम्न ताप पर पिघलता है और द्रव और ठोस दोनों अवस्थाओं में विद्युत् का कुचालक है। X है
View Solutionनिम्नलिखित में से कौन ताप पर निर्भर करता है ?
View Solutionअमोनियम कार्बामेट को गर्म करने पर यह निम्न प्रकार से अपघटित होता है: NH_(4)COONH_(2)(s) एक निश्चित ताप पर, निकाय का साम्य दाब 0.318 atm होता है, अभिक्रिया के लिए K_(p) है:
View Solution15∘C ताप और 1.5 bar दाब पर वायु का एक बुलबुला अंतर्जलीय होता है। यदि बुलबुला सतह पर आ जाता है जहाँ 25∘C ताप और 1.0 bar दाब होता है तो बुलबुले के आयतन का क्या होगा?
View Solutionयदि 25^@ C पर फ्लोराइड आयन के लिए pK_b , 10.83 है, तब इस ताप पर जल में हाइड्रोफ्लोरिक अम्ल का आयनन स्थिरांक है:
View Solution
