ऊष्मा के चालक पदार्थ से बने तथा स्थिर रखे गए बेलन की त्रिजयका R तथा ऊँचाई I0 है | बेलन नीचे से खुला है तथा इसके ऊपरी सिरे में एक छोटा छेद है, जैसा कि चित्र में दिखाया गया है | एक पिस्टन जिसका द्रव्यमान M है, ऊपरी सतह से L दुरी पर पकड़ा हुआ है | वायुमण्डलीय दाब P0 है |

जब पिस्टन ऊपरी सिरे से 2L दूरी पर है, ऊपर के सिरे में स्थित छेद को बन्द कर दिया जाता है | पिस्टन को ऐसी जगह लाकर छोड़ा जाता है जहाँ वः संतुलन में रह सकता है | इस स्थिति में ऊपरी सिरे से पिस्टन की दूरी है |
(2p0πR2πR2p0+Mg)(2L)
(p0πR2−MgπR2p0)(2L)
(p0πR2+MgπR2p0)(2L)
(p0πR2πR2p0−Mg)(2L)
The correct Answer is:D
पिस्टन को छोड़ते समय, पिस्टन की बेलन के ऊपरी सिरे से दुरी 2L है | माना पिस्टन के संतुलन की स्थिति में आने पर इसकी बेलन के ऊपरी सिरे से दुरी y है तथा बेलन दाब p है | बेलन में भरी वायु का यह प्रसार .समतापी. है क्योंकि बेलन चाक पदार्थ का बना है |
अतः सूत्र p1V1=p2V2 से,
p0(2L×πR2)=p(y×πR2)
∴p=2p0Ly
संतुलन की स्थिति में, पिस्टन के ऊपर की वायु का तथा पिस्टन का सम्मिलित भर (नीचे को कार्यरत) तथा पिस्टन पर नीचे से ऊपर की ओर लगने वाले वायुमण्डलीय दाब के कारण बल परस्पर बराबर होंगे, अर्थात
p(πR2)+Mg=p0(πR2)
p का उपरोक्त मान रखने पर,
2p0Ly=p0−MgπR2
हल करने पर, y=2p0LπR2p0πR2−Mg
Topper's Solved these Questions
- ऊष्मा एवं उष्मागतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - ऊष्मा एवं उष्मागतिकी EXERCISE - विश्लेषणात्मक प्रश्न
41 Videos
- MOCK TEST 2022BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - MOCK TEST 2022EXERCISE - प्रश्न
18 Videos
- कार्य ऊर्जा एव सामर्थ्य BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - कार्य ऊर्जा एव सामर्थ्य EXERCISE - श्रृंखलाबद्ध-बोधन प्रकार
6 Videos
Similar Questions
एक सीसे की गोली अवरोधक द्वारा रोके जाने पर पिघल जाती है | यह मानते हुए कि अवरोधक द्वारा कुल उत्पन्न ऊष्मा की 25 प्रतिशत मात्रा अवशोषित कर ली जाती है, गोली का वेग ज्ञात कीजिए (गोली का प्रारम्भिक ताप =27∘C, सीसे का गलनांक =327∘C, सीसे की विशिष्ट ऊष्मा =0.03 कैलोरी ग्राम−1−.∘C−1, सीसे के गलन की गुप्त ऊष्मा = 6 कैलोरी ग्राम−1 तथा J = 4.2 जूल कैलोरी−1)
View Solutionमान लीजिये मुक्त आकाश (free space) में एक गोलाकार गैस के बादल का द्रव्यमान घनत्व ρ(r) है तथा इसकी केन्द्र से त्रिज्य (radial) दूरी r है I यह गैसीय बादल m द्रव्यमान के समान कणों से बना है जो कि एक समकेंद्रीय वृत्ताकार कक्षाओं में समान गतिज ऊर्जा K से घूम रहे हैं। इन कणों पर पारस्परिक गुरुत्वाकर्षण बल लग रहा है। यदि ρ(r) समय के साथ एक स्थिर राशि है, तब कणों का संख्या घनत्व n(r) = ρ(r)/m का मान होगा,
[G सार्वत्रिक गुरुत्वीय नियतांक है]
View Solutionएक नत समतल के घर्षण रहित पृष्ठ पर M द्रव्यमान का एक छोटा गुटका गतिमान है, बिंदु B पर नत समतल का कोण 60∘से 30∘ अचानक परिवर्तित होता है। गुटका प्रारम्भ में बिंदु A पर विरामावस्था में है। नत समतल तथा गुटके के बिच संघट्ट अप्रत्यास्थ माना गया (g=10मीसे2)
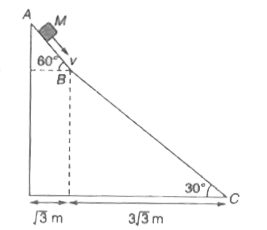
दूसरे नत समतल से टकराने के तुरंत बाद बिंदु B पर गुटके की चाल है
View Solutionमाना कि △PQR एक त्रिभुज है तथा →a=−−→QR,→b=−−→RP तथा →c=−−→PQ है | यदि |→a|=12,∣∣→b∣∣=4√3 तथा →b.→c=24 तो निम्न में से कोण-सा (से) सही है
View Solutionएक काले तथा लाल पासे को कर्म में उछाला गया है। तब
पासो पर प्राप्त अंको का योग 9 से अधिक होने कि सप्रतिबन्ध प्रायिकता ज्ञात करो यदि ज्ञात है कि काले पासे पर अंक 5 प्रकट हुआ है।
View Solutionताश के 52 पत्तो की एक सुनिश्चित गड्डी में से एक पत्ता यदृच्छया निकाला जाता है | यदि
E : निकाला गया पत्ता हुकुम का है |
F : निकाला गया पत्ता इक्का है , तो E तथा F घटनाएँ है -
View Solutionयदि एक दीर्घवृत्त जिसका केंद्र मूलबिंदु पर है, के दीर्घ कक्ष तथा लघु कक्ष कि लम्बाइयों का अंतर 10 है तथा एक नाभिकेन्द्र (0,5√3) पर है, तो इसके नाभिलम्ब की लम्बाई है
View Solutionरेखा 4x−3y+2=0 के समांतर रेखाएं खींची गई है जो मूलबिंदु 35 से की दुरी पर है, तो निम्न में से कौन-सा एक बिंदु इनमे से किसी रेखा पर स्थित है?
View Solutionएक वृत्त X-अक्ष पर एक जीवा काटता है जिसकी लम्बाई 4a है तथा यह वृत्त Y-अक्ष के एक बिन्दु से होकर जाता है जिसकी मूलबिंदु से दुरी 2b है , तो वृत्त के केन्द्र का बिन्दुपथ (locus) है
View Solutionयदि एक अतिपरवलय के शीर्ष (−2,0) तथा (2,0) पर है तथा इसकी एक नाभि (−3,0) पर है, तो निम्न में से कौन-सा बिन्दु इस अतिपरवलय पर स्थित नहीं है
View Solutionमाना एक दीर्घवृत्त कि नाभियां S तथा S' है तथा इसके लघु अक्ष का कोई एक शीर्ष B है। यदि ΔS'BS एक समकोण त्रिभुज है जिसका समकोण B पर है तथा ΔS'BS का क्षेत्रफल 8 वर्ग इकाई है, तो दीर्घवृत्त की एक नाभिलम्ब जीवा की लम्बाई है
View Solutionएक अतिपरवलय बिन्दुओं (3,2) तथा (-17,12) से गुजरता है और उसका केंद्र मूलबिन्दु पर है तथा अनुप्रस्थ अक्ष x- अक्ष है। अतिपरवलय की अनुप्रस्थ अक्ष की लम्बाई है।
View Solutionएक वस्तु जिसका द्रव्यमान m है विराम से h ऊँचाई से गुरुत्वीय त्वरण g के अन्तर्गत गिरती है तथा यह रेत में गहराई d तक धंसती है। रेत में फँसने के दौरान औसत मन्दन होगा
View Solutionजब 'r त्रिज्या का एक हवा का बुलबुला किसी झील की तली से सतह तक उठता है तो उसकी त्रिज्या 5r/4 हो जाती है (वायुमण्डलीय दाब जल स्तम्भ की 10 मीटर की ऊंचाई के बराबर है)। यदि ताप नियत है तथा पृष्ठ तनाव को उपेक्षणीय माना गया है, तो झील की गहराई है
View SolutionA cylinder of radius 4.5 cm and height 12 cm just fits in another cylinder completely with their axis perpendicular. What is the radius (in cm) of second cylinder? एक बेलन जिसकी त्रिज्या 4.5 से.मी. तथा ऊँचाई 12 से.मी. है, को एक अन्य बेलन में उनके अक्षों के लम्बवत् पूरी तरह से सम्माहित किया गया है। दूसरे बेलन की त्रिज्या (से.मी. में) क्या है?
View Solution30 बच्चो की एक कक्षा में सरन शीर्ष से 9 वे रैंक पर है| मनीष सरन से पांच रैंक निचे है| तल से मनीष की रैंक क्या है?
View Solution
