R के विभिन्न मान R1,R2,R3 है| R1,R2 तथा R3 के सांगत शून्य विक्षेप को स्थितियों क्रमश: A,B,C है| प्रतिरोध के किस मान के लिए X का मान सर्वाधिक शुद्ध होगा तथा क्यों?
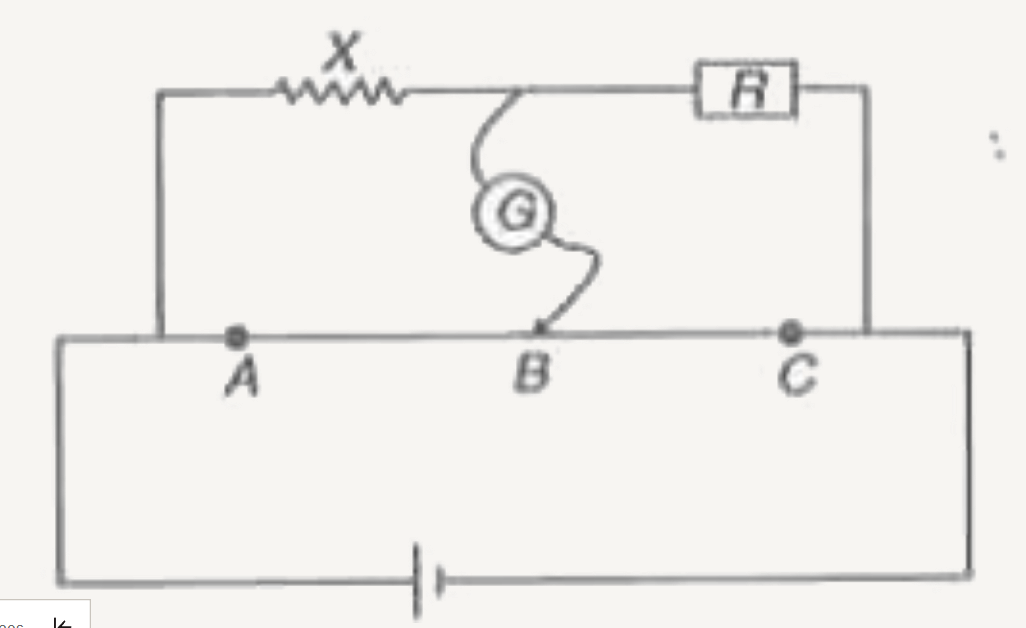
The correct Answer is:B स्थिति सर्वाधिक उपयुक्त उत्तर है|
यदि सेतु की चारों भुजाओं के प्रतिरोध समान हो तो तार सेतु सर्वाधिक संवेदनशील होता है|
Topper's Solved these Questions
- धारा वैघुतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - धारा वैघुतिकी EXERCISE - क्षृंखलाबद्ध-बोधन प्रकार (अनुछेद I )
2 Videos
- धारा वैघुतिकी BOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - धारा वैघुतिकी EXERCISE - एकल पूर्णांक उत्तर प्रकार
5 Videos
- द्रव्यमान केंद्र और सवेगBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - द्रव्यमान केंद्र और सवेगEXERCISE - श्रृंखलाबद्ध-बोधन प्रकार
3 Videos
- पदार्थ के गुणBOOK - JEE Main & Advanced (Hindi Medium)CHAPTER - पदार्थ के गुणEXERCISE - शृंखलाबद्ध-बोधन प्रकार (अनुच्छेद-IV)
2 Videos
Similar Questions
h ऊँचाई वाले निर्वातित एक बेलनाकार कक्ष के दोनों छोरो पर दो दृढ़ चालक पट्टिकाएं है और उसका वक्रपृष्ठ अचालक है, जैसा की चित्र में दर्शाया गया है। कम भार वाली मुलायम पदार्थ से बनी हुई कई गोलाकार गोलियाँ, जिनकी सतह पर एक चालक पदार्थ की परत चढ़ी है, नीचे वाली पट्टिका पर रखी हुई है। इन गोलियों की त्रिज्या r<<h है। अब एक उच्च वोल्टता का स्त्रोत इस प्रकार से जोड़ा जाता है कि नीचे वाली पट्टिका पर +V0 एवं ऊपर वाली पट्टिका पर −V0 का विभव आ जाता है। चालक परत के कारण गोलियाँ आवेशित होकर पट्टिका के साथ समविभव हो जाती है जिसके कारण वे पट्टिका से प्रतिकर्षित होती है। अंततोगत्वा गोलियाँ ऊपरी पट्टिका से टकराती है, जहाँ पर गोलियों के पदार्थ की मुलायम प्रकृति के कारण प्रत्यवस्थान गुणांक को शून्य लिया जा सकता है। कक्ष में विद्युत क्षेत्र को समानान्तर पट्टिका वाले संधारित्र के माना जा सकता है। गोलियों की एक दूसरे से पारस्परिक क्रिया एवं टकराव को नगण्य माना जा सकता है (गुरुत्वाकर्षण नगण्य है।)

निम्नलिखित में से कौनसा कथन सत्य है?
View Solutionजब दो अभिन्न बैटरियों को, जिनमे से प्रत्येक का आंतरिक प्रतिरोध 1Ω है, श्रेणीक्रम में जोड़कर R प्रतिरोध पर लगते है, तो R में उत्पन्न ऊष्मा की दर J1 है| यदि दो बैटरियों को समान्तर क्रम में लगाकर R प्रतिरोध पर लगाने पर उत्पन्न ऊष्मा की दर, J2 है| यदि J1=2.25J2, तब R का मान Ω में कितना होगा?
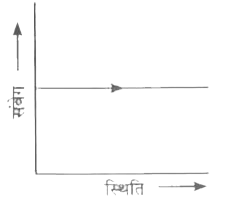
View Solutionहर प्रकार की गतिकीय समस्याओं के निश्लेषण के लिए कला-समष्टि चित्रा (Phase space diagrams) का उपयोग किया जाता है। प्रारम्भिक दशा, स्थिति व संवेग में बदलाव होने पर इनका उपयोग चालन में उत्पन्न बदलावों को समझने में बहुत उपयोगी है। यहाँ हम एकविमीय सरल गतिकीय निकायों की बात करते हैं। इनके लिए कला-समष्टि समतल है जिसमें स्थिति X-अक्ष पर तथा संबेग Y-अक्ष पर रखते हैं, तब कुला-समष्टि चित्र इस समतल में एक x(t)-p(t) वक्र होगा। वक्र पर तीर समय बढ़ने की दिशा को दर्शाता है।
उदाहरण के लिए, स्थिर वेग से चल रहे कण के लिए कला- समष्टि चित्रा है, सरल रेखा है, जिसे चित्र में दिखाया गया है। चिह्न परिपाटी में स्थिति या संवेग को ऊपर (या दाहिने) ओर धनात्मक तथा नीचे (या बाई) ओर ऋणात्मक माना जाता है।
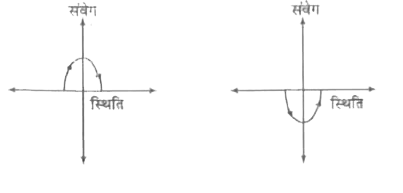
1. जमीन से ऊपर की ओर फेंकी गई गेंद का कला-समष्टि चित्रा है।
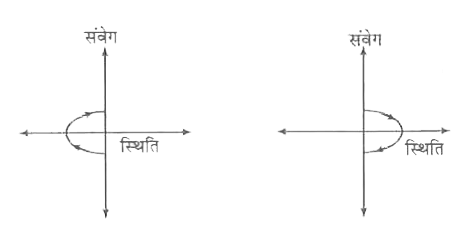
View Solutionचित्र में दिखाई गयी पिचकारी में एक पिस्टन वायु को एक चंचू द्वारा बाहर धकेलता है। चंचू के सामने एकसमान अनुप्रस्थ-काट वाली पतली नली लगी है। नली का दूसरा सिरा द्रव से भरे एक छोटे पात्र में है। जब पिस्टन वायु को चंचू से बाहर धकेलता है, तब पात्र में द्रव उठकर चंचू में आ जाता है। ओर फुहार के रूप में बाहर निकलता है। चित्र में दिखाई गयी पिचकारी में पिस्टन तथा चंचू की त्रिज्याएँ क्रमशः 20 मिमी तथा मिमी है। पात्र का ऊपरी भाग वातावरण में खुला है।

पिस्टन को 5 मिमी/से की गति से धकेलने पर चंचू से बाहर वाली वायु की गति है
View Solution(r_(3)+r_(1))(r_(3)+r_(2))sin C=2r_(3)sqrt(r_(2)r_(3)+r_(3)r_(1)+r_(1)r_(2))
View SolutionProve that r1r2+r2r3+r3r1=14(a+b+c)2
View SolutionStatement I In a ΔABC,ifa<b<c and ri si inradius and r1,r2+r2r3 are the exradii opposite to angle A,B,C respectively, then r<r1<r2<r3.
Statement II For, ΔABCr1r2+r2r3+r3r1=r1r2r3r
View Solutionshow that r2r3+r3r1+r1r2=s2
View SolutionProve that r1(r2+r3)√r1r2+r2r3+r3r1=a
View SolutionIf rr1=r2r3, then
View SolutionStatement-1: ln !ABC,r1+r2+r3−r=4R
Statement-2: In !ABC,r1r2+r2r3+r3r1=!2
View SolutionProve the questions
a(rr1+r2r3)=b(rr2+r3r1)=c(rr3+r1r2)
View SolutionIf r1,r2,r3,r are in usual notation in ΔABC then r1r2r3−r(r1r2+r2r3+r3r1)=
View Solutionk के किस मान के लिए सारणिक ∣∣∣k24−3∣∣∣ का मान शुन्य होगा ?
View SolutionProve that r1r2+r2r3+r3r1=14(a+b+c)2
View SolutionIf rr2=r1r3 then
View Solution
