Among the 8! [permutations of the digits 1, 2, 3..., 8, consider those arrangements which have the following property. If we take any five consecutive positions the product of the digits in these positions is divisible by 5. The number of such arrangements is equal to a. 7! b. 2.(7!) c. ^7C4 d. none of these
To solve the problem, we need to determine how many arrangements of the digits 1 through 8 have the property that the product of any five consecutive digits is divisible by 5. The only digit among 1 to 8 that is divisible by 5 is the digit 5 itself.
1. Identify the Key Condition:
Since we need the product of any five consecutive digits to be divisible by 5, at least one of those five digits must be 5.
2. Determine the Positions of 5:
If we consider any five consecutive positions in the arrangement, the digit 5 must occupy one of those positions. For example, if we denote the positions as P1, P2, P3, P4, P5, P6, P7, P8, then:
- If 5 is in P1, it can contribute to the products of (P1, P2, P3, P4, P5).
- If 5 is in P2, it can contribute to the products of (P1, P2, P3, P4, P5) and (P2, P3, P4, P5, P6).
- This pattern continues until P4, where it can contribute to (P4, P5, P6, P7, P8).
Thus, the digit 5 must be in one of the positions P1, P2, P3, or P4.
3. Count the Valid Positions for 5:
The digit 5 can occupy any of the first four positions (P1, P2, P3, or P4). This gives us 4 possible choices for placing the digit 5.
4. Arrange the Remaining Digits:
After placing the digit 5, we have 7 remaining digits (1, 2, 3, 4, 6, 7, 8) to arrange. The number of ways to arrange these 7 digits is given by 7!.
5. Calculate the Total Arrangements:
Since there are 4 choices for the position of the digit 5 and 7! ways to arrange the remaining digits, the total number of arrangements is:
Total arrangements=4×7!=2×(2×7!)=2×7!
Conclusion:
Thus, the number of arrangements of the digits 1 through 8 such that the product of any five consecutive digits is divisible by 5 is 2×7!.
Final Answer:
The correct answer is b. 2×7!.
Since we need the product of any five consecutive digits to be divisible by 5, at least one of those five digits must be 5.
If we consider any five consecutive positions in the arrangement, the digit 5 must occupy one of those positions. For example, if we denote the positions as P1, P2, P3, P4, P5, P6, P7, P8, then:
- If 5 is in P1, it can contribute to the products of (P1, P2, P3, P4, P5).
- If 5 is in P2, it can contribute to the products of (P1, P2, P3, P4, P5) and (P2, P3, P4, P5, P6).
- This pattern continues until P4, where it can contribute to (P4, P5, P6, P7, P8).
The digit 5 can occupy any of the first four positions (P1, P2, P3, or P4). This gives us 4 possible choices for placing the digit 5.
After placing the digit 5, we have 7 remaining digits (1, 2, 3, 4, 6, 7, 8) to arrange. The number of ways to arrange these 7 digits is given by 7!.
Since there are 4 choices for the position of the digit 5 and 7! ways to arrange the remaining digits, the total number of arrangements is:
Total arrangements=4×7!=2×(2×7!)=2×7!
Thus, the number of arrangements of the digits 1 through 8 such that the product of any five consecutive digits is divisible by 5 is 2×7!.
The correct answer is b. 2×7!.
Similar Questions
How many positive integers less than 1000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3 ?
View SolutionHow many positive integers less than 1000 have the property that the sum of the digits of each such number is divisible by 7 and the number itself is divisible by 3?
View Solution
Knowledge Check
The number of ways in which we can arrange the digit 1, 2, 3, …, 9 such that the product of five digits at any of the five consecutive positions is divisible by 7 is
A7!B9P7C8!D5(7!)Five digit numbers divisible by 9 are to be formed by using the digits 0 1 2 3 4 7 8 The total number of such numbers is equal to
A216B214C212D200Digits 2, 3, 4, 6, 7, 8 are arranged in the following blanks :
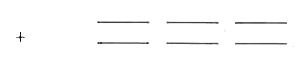
The largest possible number after addition isA1308B808C1605D1560
A five-digit number is written down at random. The probability that the number is divisible by 5 and no two consecutive digits are Identical is a. 15 b. 15(910)3 c. (35)4 d. none of these
View SolutionThe number of 4 digit numbers greater than 5,000 can be formed out of the digits 3,4,5.6 and 7(no. digit is repeated). The number of such is: a) 72 b) 27 c) 70 d) none of these
View SolutionSeven digit numbers are formed using digits 1, 2, 3, 4, 5, 6, 7, 8, 9 without repetition. The probability of selecting a number such that product of any 5 consecutive digits is divisible by either 5 or 7 is P. Then 12P is equal to
View SolutionWhich one of the following is the number by which the product of 8 consecutive integer is divisible ? 4 ! (b) 6 ! (c) 7 ! (d) 8 ! (e) All of these
View SolutionIn the case of how many digits in the number 7214658, their position in the number and the position when the digits of the numbers are arranged in the ascending order is identical ?
1) Three
2) Four
3) One
4) Two
5) None of these
View Solution
