Equation of curve in polar coordinates is $\frac{I}{r} = 2 {sin}^{2} \frac{θ}{2}$ then it represents

a straight line

a parabola

a circle

an ellipse

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Class 12 MATHS PARABOLA, ELLIPSE AND HYPERBOLA

Topper's Solved these Questions

BOOK - SIA PUBLICATIONCHAPTER - PAIR OF STRAIGHT LINES EXERCISE - PROBLEM
42videos
PAIR OF STRAIGHT LINES
BOOK - SIA PUBLICATIONCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Problems
41videos
PERMUTATIONS AND COMBINATIONS

Knowledge Check

Question 1 - Select One
A point has polar coordinate $(2, 60^{\circ})$ The same point can be represented by
A $(- 2, 240^{\circ})$
B $(2, 240^{\circ})$
C $(- 2, 60^{\circ})$
D $(2, - 60^{\circ})$
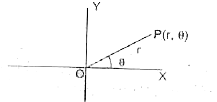
Question 2 - Select One
Let $O P = r and ∠ X O P = θ$ then the position of P in polar coordinate system is represented by $(r, θ)$ OX and O are called the initial line and pole respectively.
If p be the length of perpendicular from origin to line and if $α$ is the angle which the perpendicular to the line makes with the initial line . The equation of line is given by r $cos (θ - α) = p$

The polar coordinates of the foot of perpendicular from the pole on the line joining the two points $(r_{1}, θ_{1}) and (r_{2}, θ_{2})$ are
A $⎡ ⎢ ⎢ ⎣ \frac{r_{1} r_{2} sin (θ_{2} - θ_{1})}{\sqrt{r_{1}^{2} + r_{2}^{2} - 2 r_{1} r_{2} cos (θ_{1} - θ_{2})}}, {tan}^{- 1} (\frac{r_{1} {cos θ}_{1} - r_{2} {cos θ}_{2}}{r_{2} {sin θ}_{2} - r_{1} {sin θ}_{2}}) ⎤ ⎥ ⎥ ⎦$
B $⎡ ⎢ ⎢ ⎣ \frac{r_{1} r_{2} sin (θ_{2} + θ_{1})}{\sqrt{r_{1}^{2} + r_{2}^{2} - 2 r_{1} r_{2} cos (θ_{1} - θ_{2})}}, {tan}^{- 1} (\frac{r_{1} {cos θ}_{1} - r_{2} {cos θ}_{2}}{r_{2} {sin θ}_{2} - r_{1} {sin θ}_{1}}) ⎤ ⎥ ⎥ ⎦$
C $⎡ ⎢ ⎢ ⎣ \frac{- r_{1} r_{2} sin (θ_{2} - θ_{1})}{\sqrt{r_{1}^{2} + r_{2}^{2} - 2 r_{1} r_{2} cos (θ_{1} - θ_{2})}}, {tan}^{- 1} (\frac{r_{1} {cos θ}_{1} - r_{2} {cos θ}_{2}}{r_{2} {sin θ}_{2} - r_{1} {sin θ}_{1}}) ⎤ ⎥ ⎥ ⎦$
Dnone of these
Question 3 - Select One
Let $O P = r and ∠ X O P = θ$ then the position of P in polar coordinate system is represented by $(r, θ)$ OX and O are called the initial line and pole respectively.
If p be the length of perpendicular from origin to line and if $α$ is the angle which the perpendicular to the line makes with the initial line . The equation of line is given by r cos $(θ - α) = p$

Perpendicular distance from pole to the line $\frac{l}{r} = 4 cos θ + 2 sin θ$ is
A $2 \sqrt{5}$
B $\frac{l}{2 \sqrt{5}}$
C $\frac{2 \sqrt{5}}{l}$
Dnone of these