y=sin(mSin−1x)⇒(1−x2)y2−xy1=Solution in Telugu
m2y
−m2y
2m2y
−2m2y
The correct Answer is:B
Step by step video, text & image solution for y = sin (m Sin ^(-1)x ) implies ( 1- x ^(2)) y _(2) - xy _(1) = by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- DIFFERENTIATION BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIFFERENTIATION EXERCISE - SET-2
4 Videos
- DIFFERENTIATION BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIFFERENTIATION EXERCISE - SET-3
5 Videos
- DIFFERENTIATION BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIFFERENTIATION EXERCISE - EXERCISE 1C
3 Videos
- DIFFERENTIAL EQUATIONSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Exercise 2
15 Videos
- DIRECTION COSINES AND DIRECTION RATIOSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIRECTION COSINES AND DIRECTION RATIOSEXERCISE - EXERCISE 2 SET -2
3 Videos
Similar Questions
1.ifF(X)=1xthenf'(1)=A2.Iff(x)=x+1x+3thenf'(−1)=B3.Iff(x)=x2thenf'(1)=C4.Iff(x)=logxthenf'(3)=D
The ascending order of A,B,C ,D is
View SolutionMatch the following
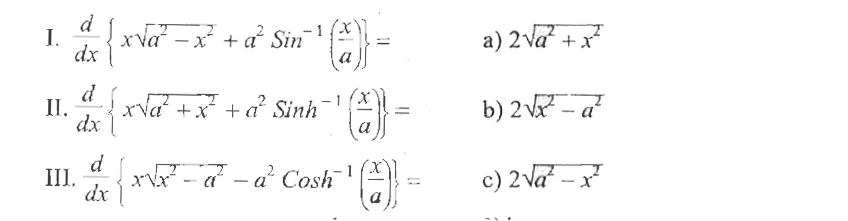
View SolutionThe function y=Sin−1(cosx) is not differentiable at
View SolutionI: The differential equation for the family of curves x2+y2−2ay=0, where a is an arbitraryconstantis (x2−y2)y'=2xy
II : The differential equation of the family of parabolas having vertices at the origin and foction y-axis is dydx=2yx
View SolutionIf the d.c.'s are (l, m, n) whose d.r's of a ray are (3, -4, 12) then ascending order of l, m, n is
View Solutionsin x + sin y = (1) / (4), sin x-sin y = (1) / (5) rArr4cot (xy) / (2) =
View Solutionif y=sin−1x√1−x2 then prove that (1−x)2.ddx=xy+1
View Solutionयदि y=sin1x√1+x2 तो सिद्ध कीजिये कि (1−x2)dydx=xy+1
View Solutionयदि y=sin−1x√(1−x2). तब सिद्ध कीजिए की,
(1−x2)dydx=xy+1
View Solutionयदि y=sin−1x√1−x2 है, तो सिद्ध कीजिए कि (1−x2)dydx=xy+1.
View Solutionsin−1x+sin−1y=cos−1{√(1−x2)(1−y2)−xy}
View SolutionIf y=e2sin−1x then ∣∣ ∣∣(x2−1)y''+xy'y∣∣ ∣∣ is equal to
View Solutiony=Sin−1x⇒(1−x2)d2ydx2=
View SolutionIf y=sin(7Sin−1x) then (1−x2)y2−xy1=
View SolutionShow that y=sin(msin−1x) is a solution of the differential equation (1−x2)y''+xy'+m2y=0
View Solution
