A:Ify=xy then dydx=y2x(1−logy)
If y=f(x)y, thendydx=y2f'(x)f(x)[1−ylogf(x)]=y2f'(x)f(x)[1−logy] Solution in Telugu
Both A and R are true R is correct reason of A
Both A and R are treu R is not correct reason of A
A is true but R is false
A is false but R is true
The correct Answer is:A
Step by step video, text & image solution for A: If y = x ^(y) then (dy)/(dx) = (y ^(2))/(x(1- log y )) If y = f (x) ^(y), then (dy)/(dx) = (y ^(2) f '(x))/(f (x) [1- ylog f (x)])= (y ^(2) f'(x))/(f (x) [1- log y]) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIFFERENTIATION EXERCISE - SET-35videos
DIFFERENTIATION
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Exercise 215videos
DIFFERENTIAL EQUATIONS
- BOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - DIRECTION COSINES AND DIRECTION RATIOSEXERCISE - EXERCISE 2 SET -23videos
DIRECTION COSINES AND DIRECTION RATIOS
Similar Questions
Match the following
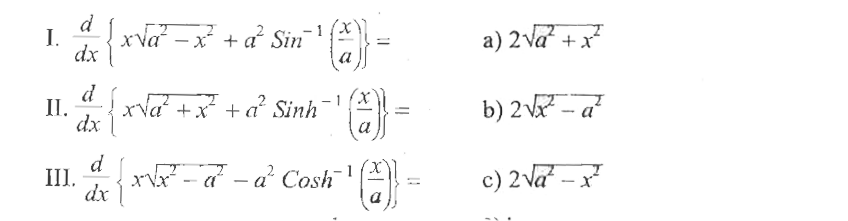 03:55View Solution
03:55View SolutionI: The differential equation for the family of curves x2+y2−2ay=0, where a is an arbitraryconstantis (x2−y2)y'=2xy
II : The differential equation of the family of parabolas having vertices at the origin and foction y-axis is dydx=2yx03:27View SolutionIf the d.c.'s are (l, m, n) whose d.r's of a ray are (3, -4, 12) then ascending order of l, m, n is
03:02View SolutionIf f(x)=cos(logx), then f(x)f(y)−12[f(xy)+f(xy)]=
02:24View SolutionIf f(x)=cos(logx), then f(x)f(y)−12[f(xy)+f(xy)]=
08:44View SolutionIf f^(1)(x)=(1)/(1+(ln x)^(2)) and y=f(e^(tan x)) then (dy)/(dx) is equal to
02:59View SolutionIf f(x)=cos(logx), then f(x2)f(y2)−12[f(x2y2)+f(x2y2)] has the value
01:38View Solutionयदि f(x) = cos(log x), तो f(x2)f(y2)−12[f(x2y2)+f(x2y2)] का मान है-
03:30View SolutionIf (√x)(√x)(√x)...∞ and xdydx=f(y)2−ylogx, then the value of f(y) is -
03:30View SolutionIf y=f(x)+1y, then dydx=y2f'(x)1+y2
02:02View SolutionIf x+y=tan−1y and d2ydx2=f(y)dydx, then f(y)=
03:30View SolutionIf x+y=tan−1y and d2ydx2=f(y)dydx, then f(y)=
01:12View SolutionIf x+y=tan−1y and d2ydx2=f(y)dydx then f(y)=
01:37View Solutionf(x) = cos (log x) అయితే f(1x)f(1y)−12[f(xy)+f(xy)]=0 అని చూపండి.
03:16View Solutionনীচের প্রদত্ত বিবৃতিটি ঠিক না ভুল: y=log(f(x)) হলে dydx=1f(x)log(f(x))
05:39View Solution

