Let S be the sample space of the random experiment of throwing simultaneously two unbaised dice with six faces (numbered 1 to 6) and let E1={(a,b), ε S:ab =k} for k≥1Solution in Telugu
p1<p30<p6
p36<p6<p2<p4
p1<p14<p4<p6
p36<p11<p6<p4
The correct Answer is:A
Step by step video, text & image solution for Let S be the sample space of the random experiment of throwing simultaneously two unbaised dice with six faces (numbered 1 to 6) and let E_(1)={(a,b), epsi S:ab =k} for kge 1 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBABILITYBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - PROBABILITYEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET-3
9 Videos
- PROBABILITYBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - PROBABILITYEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET-4
5 Videos
- PROBABILITYBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - PROBABILITYEXERCISE - EXERCISE 2 (SPECIAL TYPE QUESTIONS) SET-1
6 Videos
- PERMUTATIONS & COMBINATIONSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - PERMUTATIONS & COMBINATIONSEXERCISE - EXERCISE 2 ( SPECIAL TYPE QUESTIONS ) SET -4
10 Videos
- PRODUCTS OF VECTORSBOOK - DIPTI PUBLICATION ( AP EAMET)CHAPTER - PRODUCTS OF VECTORSEXERCISE - Exercise 2 (Special Type Questions) SET -D
14 Videos
Similar Questions
Match the following
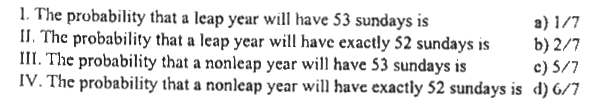
View SolutionA: There are 4 letters and 4 addressed envelopes. If the letters are put in the random in the envelopes , the probability that all the letters may be placed in wrongly addressed envelopes is 3/8.
R: If n letters are put at random in the n addressed envelopes , the probability that all the letters may be in wrong envelopes = 1-11!+12!−13!+.....+(−1)nn!
View Solution1:20 persons among whom A and B sit in random along a round table. The probability that there are 6 persons between A and B is 2/19.
II: Out of 30 consecutive integers 2 are drawn at random. The probabilty that their sum is odd is 15/29.
View SolutionA : the number of ways in which 5 boys and 3 girls can sit in a row so that two girls come together is 5!6P5
R : the number of ways of ways in which m ( first type of different ) things and n ( second type of different ) things (m+1≥n) can be arranged in a row so that no two things of second kind come together is m! (m+1)Pn
View SolutionA : Angle between the vectors I - 2j + k, 2i - j - k is π3.
R : If θ is the angle between a,b then cos θ=a.b|a||b|
View SolutionLet S be the sample space of the random experiment of throwing simultaneously two unbiased dice with six faces (numbered 1 to 6 ) and let E_(k)={(a,b)in S:ab=k} for k>=1 If p_(k)=p(E_(k)) for k>=1 then correct among the following,is (Eamcet 2008)
View SolutionIf E be a random experiment or rolling a dice and S be its sample space, then if one dice is rolled then find the sample space of it.
View SolutionIf E be a random experiment or rolling a dice and S be its sample space, then if one dice is rolled
If two dice are rolled, find the sample space.
View SolutionLet two fair six faced dice A and B be thrown simultaneously. If E1 is the event that die A shows up four, E2 is the event that die B shows up two and E3 is the event that the sum of numbers on both dice is odd, then which of the following statements is NOT true?
View SolutionLet two fair six-faced dice A and B be thrown simultaneously . If E1 is the event that die A shows up four , E2 is the event that die B shows up two E3 is the event that the sum of numbers on both dice is odd, then which of the following statements is not true ?
View SolutionLet S be the sample space of the random experiment of throwing simultaneously two unbaised dice with six faces (numbered1 to 6) and let Ek={(a,b)∈S:ab=k}fork≥1. If Pk=P(Ek)fork≥1 then the correct, among the following is
View Solutionमाना S एक प्रयोग के लिए एक साथ फेंके गए दो अनभिनत पांसे जिनके छ: फलक है (1 से 6 तक अंक अंकित है), की यादृच्छिक प्रतिदर्श समष्टि है एवं माना Ek={(a,b)∈S:ab=k}, k≥1 के लिए। यदि pk=P(Ek), k≥1 के लिए, तब निम्नलिखित में से सत्य है
View SolutionThe number of outcomes in the sample space of the random experiment of throwing two dice is....a)6^3
View SolutionConsider the random experiment of throwing two dice together Write the sample space of the experiment
View SolutionThe number of outcomes in the sample space of the random experiment
of throwing two dice is………
View Solution
