Prove that the quadrilateral formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
Let a,B,c and D be the position vector Of A,b,,c and D.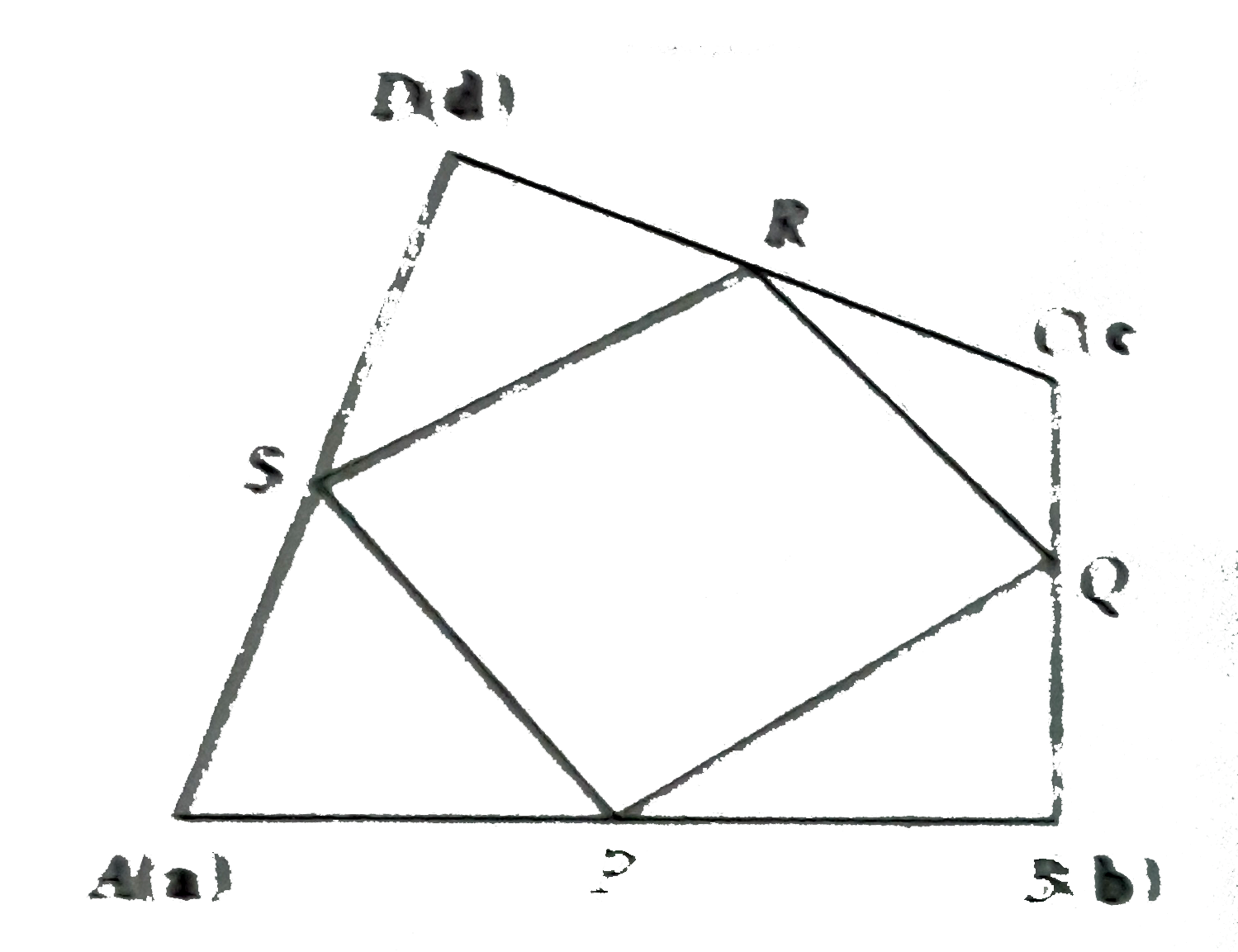
Hence , position vector of mid -points P,Q, R and s will be
=b+c2,b+c2,c+d2andd+a2
We have ,
PQ= position vector of Q-position vector of P
=b+c2−a+b2=c−a2
and SR= postion vector of R- position vector of S
=c+d2−d−a2=c−a2
From Eq.(i)and (ii),We get
PQ=SR
QR=PS
∴PQRS is a parallelogram.
Topper's Solved these Questions
Similar Questions
Prove that the figure formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
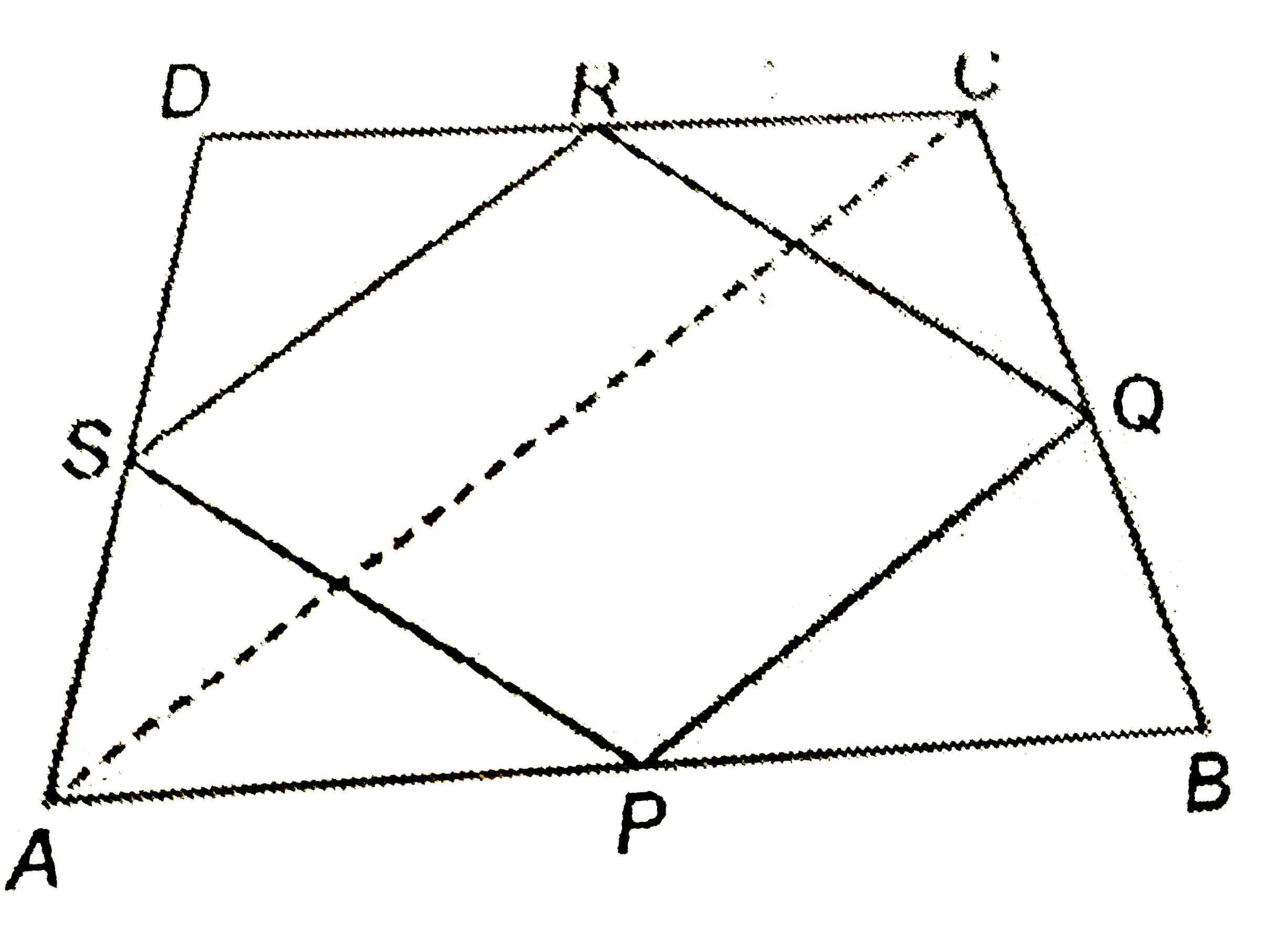
View SolutionProve that the figure formed by joining the mid-points of the pair of consecutive sides of a quadrilateral is a parallelogram. OR BACD is a parallelogram in which P,Q,R and S are mid-points of the sides AB,BC,CD and DA respectively. AC is a diagonal. Show that : PQ∣∣AC and PQ=12AC SR∣∣AC and SR=12AC PQ=SR (iv) PQRS is a parallelogram.
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.
View SolutionThe diagonals of a quadrilateral ABCD are mutually perpendicular . Prove that the quadrilateral formed by joining the mid-points of its consecutive sides is a reactangle.
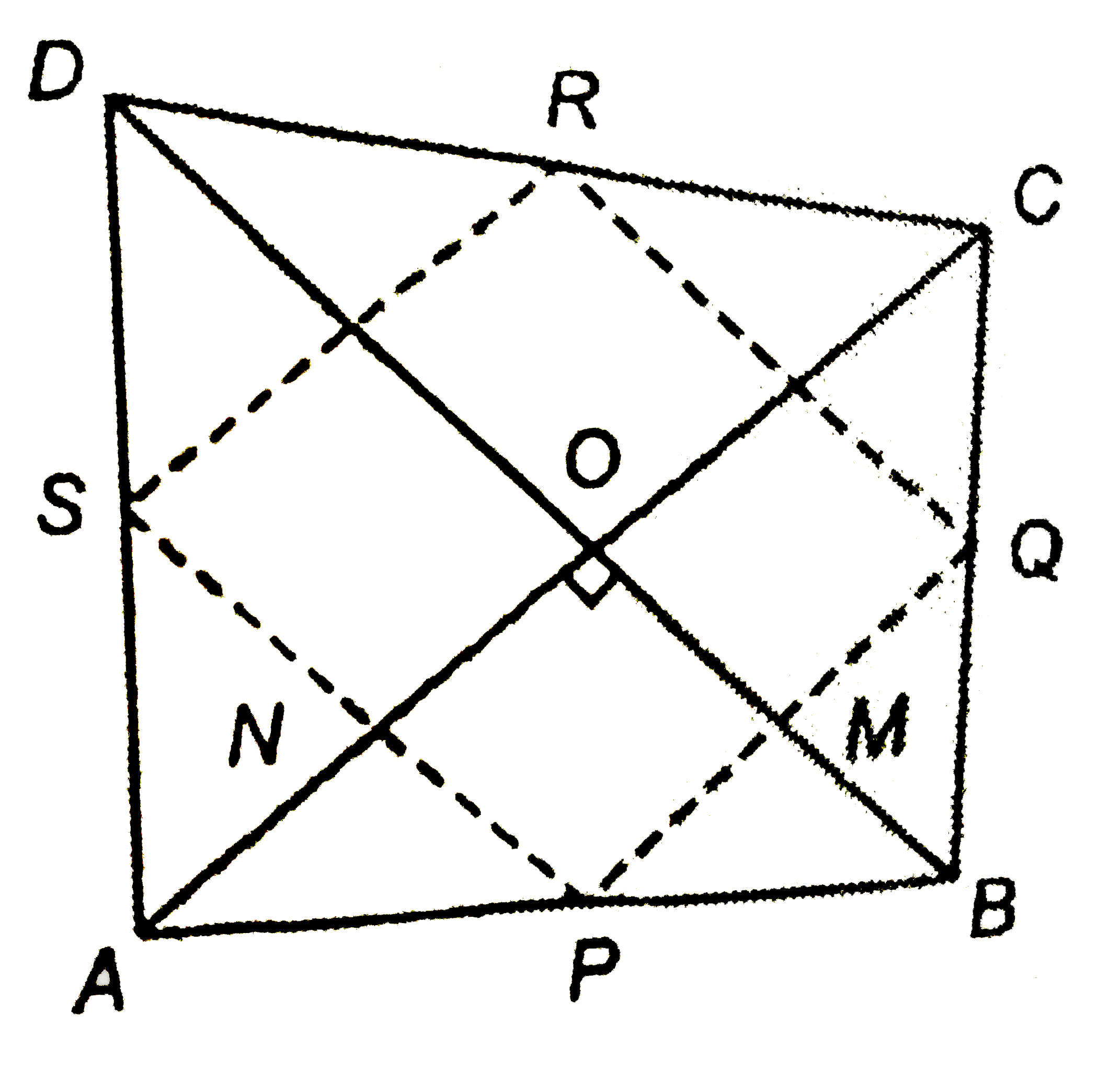
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square, is also a square.
View SolutionShow that the quadrialteral formed by joining the mid-points of the consecutive sides of a rhombus, is a rectangle.
View SolutionThe quadrilateral formed by joining the mid-points of the sides AB, BC, CD, DA of a quadrilateral ABCD is
View Solution
