A bead can slide on a smooth circular wire frame of radius r which is fixed in a vertical plane. The bead is displaced slighty from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the verticle line is
√2gr
√2gr(1−sinθ)
√2gr(1−cosθ)
2√gr
The correct Answer is:C
(c ) h=r(1−cosθ)
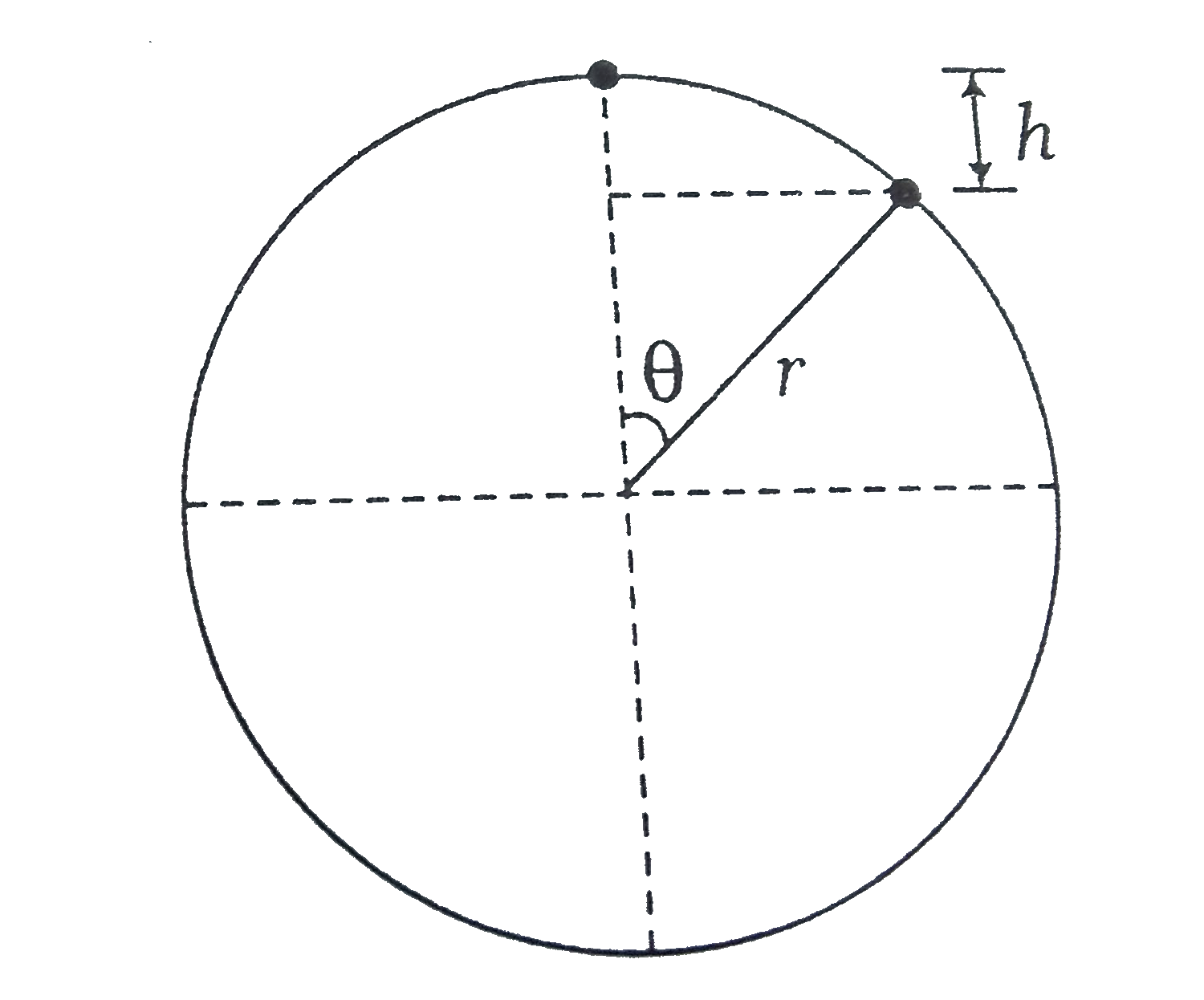
Now,decrease in PE =increase in KE
or mgr(1−cosθ)=12mv2 or v=√2gr(1−cosθ)
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRANCE SPECIAL QUESTIONS16videos
WORK, ENERGY AND POWER
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MATCH THE COLUMNS7videos
WORK, ENERGY AND POWER
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - CHECK POINT 6.310videos
WORK, ENERGY AND POWER
- BOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based2videos
WORK, ENERGY & POWER
- BOOK - DC PANDEYCHAPTER - WORK, POWER AND ENERGYEXERCISE - E Integer Type Questions11videos
WORK, POWER AND ENERGY
Similar Questions
A small 100g sleeve B can slide on a smooth, circular and rigid wire frame A of radius 5m placéd in vertical plane. The wire frame is rotating about its vertical diameter at 2rads. When the sleeve is brought at a particular angular position other than the bottom and the top of the ring, the sleeve will not slide on the wire frame. What is force of interaction (in N) between the sleeve and the wire frame at this position?
'(##CEN_KSR_PHY_JEE_C07_020_Q11##)'View SolutionA bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.
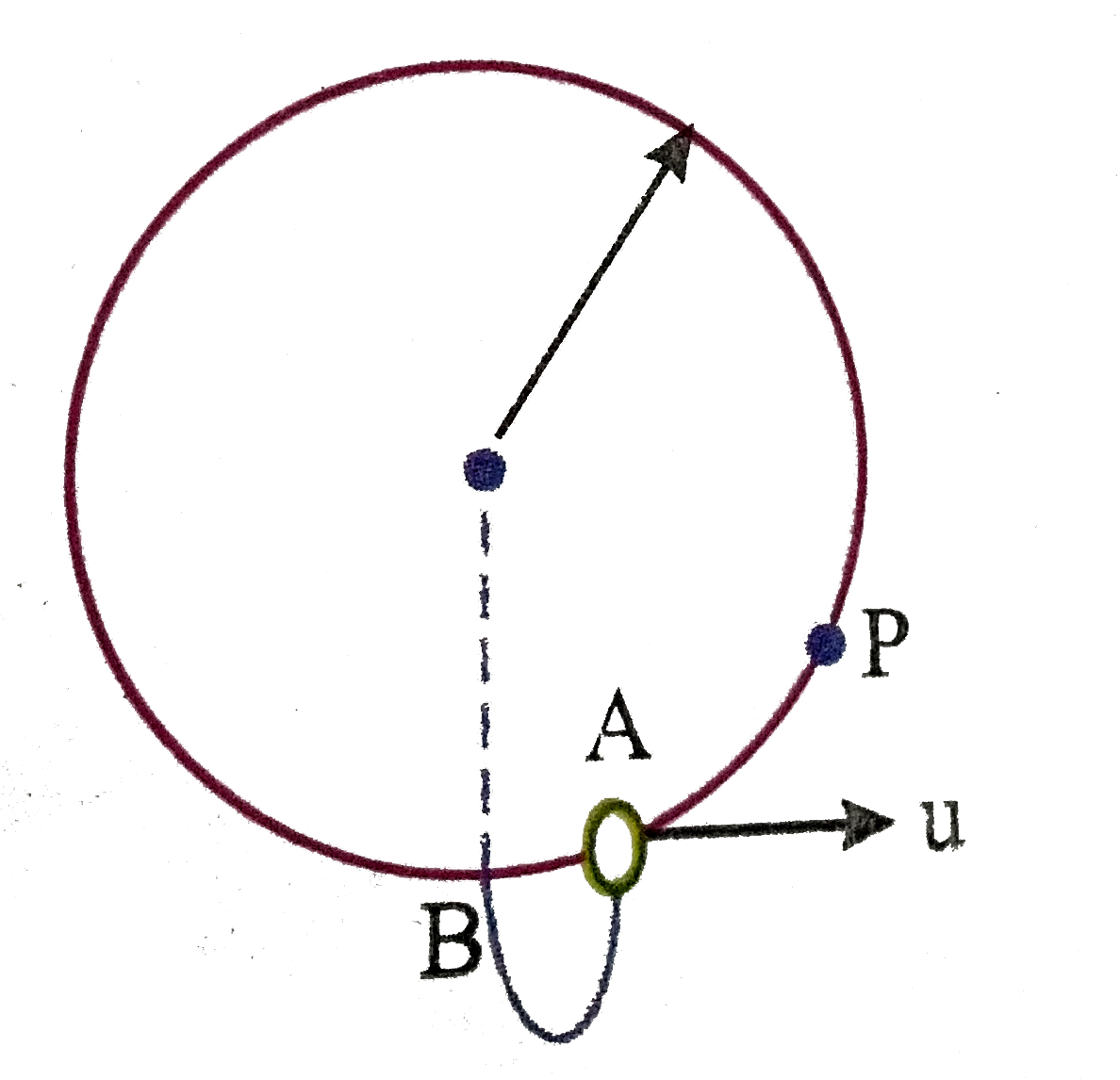
The elastic energy stored in the string when the bead is at the highest point B will beView Solution
Knowledge Check
- Question 1 - Select One
A bead can slide on a smooth circular wire frame of radius R which is fixed in a vartical plane. The bead is displaced slightly from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle θ made by the bead with the vertical line is
A√2gRB√2gR(1−sinθ)C√2gR(1−cosθ)D2√gR - Question 2 - Select One or More
A bead is free to slide down a smooth wire tightly stretched between points A and B on a vertical circle. If the starts from rest at A, the heighest point on the circle
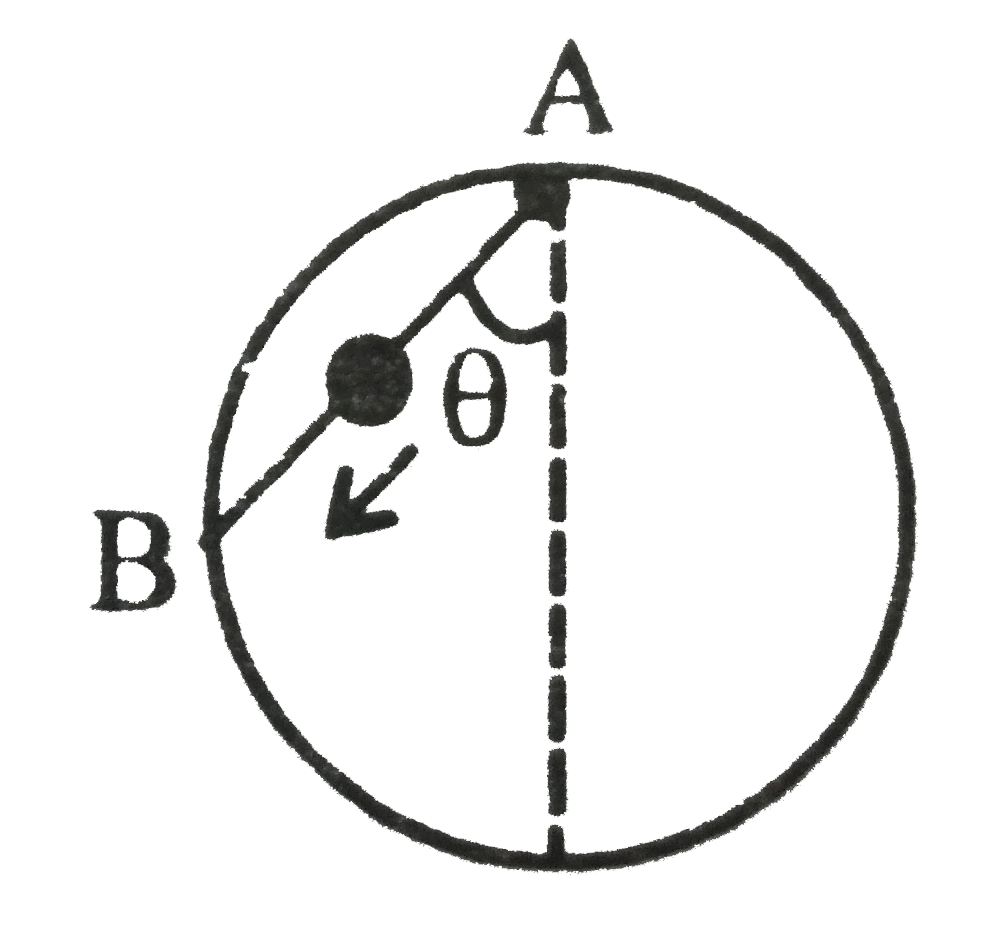 Aits velocity v on arriving at b is proportional to cosθBits velocity v on arriving at B is proportional to tanθCtime to arrive at B is proportional to cosθDtime to arrive at B is independent of θ
Aits velocity v on arriving at b is proportional to cosθBits velocity v on arriving at B is proportional to tanθCtime to arrive at B is proportional to cosθDtime to arrive at B is independent of θ - Question 3 - Select One
A bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.

If v=2u0, the tension T in th elastic string when the bead is at the highest point B of the wire isA3μ20aB4mgC2mgD(4u20a−g)m
A bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.
The smallest value u0 of u for which the bead will make complete revolutions of the wire will beView SolutionTwo beads A and B of masses m1 and m2 respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. B is stationary at the lowest point when A is gently dislodged from rest at the highest point. A collided with B at the lowest point. The impulse given to B due to collision is just great enough to carry it to the level of the centre of the circle while A is immediately brought to rest by the impact.
 What is the coefficient of restituting between the beads?View Solution
What is the coefficient of restituting between the beads?View SolutionTwo beads A and B of masses m1 and m2 respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. B is stationary at the lowest point when A is gently dislodged from rest at the highest point. A collided with B at the lowest point. The impulse given to B due to collision is just great enough to carry it to the level of the centre of the circle while A is immediately brought to rest by the impact.

Find the ratio m1:m2View SolutionTwo beads A and B of masses m1 and m2 respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. B is stationary at the lowest point when A is gently dislodged from rest at the highest point. A collided with B at the lowest point. The impulse given to B due to collision is just great enough to carry it to the level of the centre of the circle while A is immediately brought to rest by the impact.

If m2 again comes down and collides with m1 then after the collisionView SolutionA wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
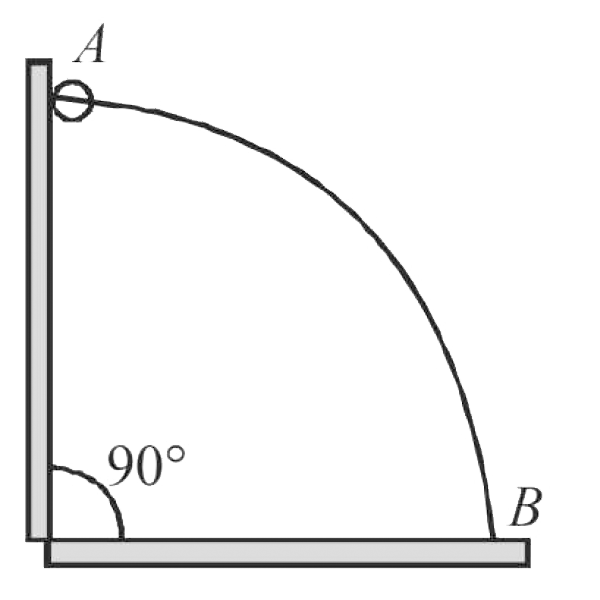 View Solution
View Solution

