A uniform circular disc of radius R oscillates in a vertical plane about a horizontal axis. Find the distance of the axis of rotation from the centre of which the period is minimum. What is the value of this period?
To solve the problem of finding the distance of the axis of rotation from the center of a uniform circular disc that oscillates in a vertical plane about a horizontal axis, we will follow these steps:
Step 1: Understand the Moment of Inertia
The moment of inertia I of a uniform circular disc about an axis through its center and perpendicular to its plane is given by:
I=12mR2
where m is the mass of the disc and R is its radius.
Step 2: Use the Parallel Axis Theorem
To find the moment of inertia about an axis that is a distance d from the center, we use the parallel axis theorem:
Id=I+md2=12mR2+md2
Step 3: Determine the Period of Oscillation
The period T of oscillation for a physical pendulum is given by:
T=2π√Idmgd
Substituting Id from the previous step, we get:
T=2π
⎷12mR2+md2mgd
Step 4: Simplify the Period Expression
We can simplify the expression for the period:
T=2π√R2/2+d2gd
Step 5: Minimize the Period
To find the minimum period, we need to minimize the expression inside the square root. This involves taking the derivative with respect to d and setting it to zero:
ddd(R2/2+d2d)=0
This leads to the condition:
R2/2+d2−(R2/2+d2)=0
Solving this gives:
d=R√2
Step 6: Calculate the Minimum Period
Substituting d=R√2 back into the period formula:
T=2π
⎷R2/2+(R/√2)2g(R/√2)
This simplifies to:
T=2π√R2gR/√2=2π√R√2g
Final Result
Thus, the distance of the axis of rotation from the center for minimum period is:
d=R√2
And the minimum period is:
Tmin=2π√R√2g
The moment of inertia I of a uniform circular disc about an axis through its center and perpendicular to its plane is given by:
I=12mR2
where m is the mass of the disc and R is its radius.
To find the moment of inertia about an axis that is a distance d from the center, we use the parallel axis theorem:
Id=I+md2=12mR2+md2
The period T of oscillation for a physical pendulum is given by:
T=2π√Idmgd
Substituting Id from the previous step, we get:
T=2π
⎷12mR2+md2mgd
We can simplify the expression for the period:
T=2π√R2/2+d2gd
To find the minimum period, we need to minimize the expression inside the square root. This involves taking the derivative with respect to d and setting it to zero:
ddd(R2/2+d2d)=0
This leads to the condition:
R2/2+d2−(R2/2+d2)=0
Solving this gives:
d=R√2
Substituting d=R√2 back into the period formula:
T=2π
⎷R2/2+(R/√2)2g(R/√2)
This simplifies to:
T=2π√R2gR/√2=2π√R√2g
Thus, the distance of the axis of rotation from the center for minimum period is:
d=R√2
And the minimum period is:
Tmin=2π√R√2g
Similar Questions
A uniform disc of radius R=13cm can rotate about a horizontal axis perpendicular to its plane and passing through the edge of the disc. Find the period of small oscillations of that disc if the logarithmic damping decrement is eqal to λ=1.00.
View SolutionA uniform square amina of side 0.3m oscillates ina vertiacla plane about an axis perpendicular to the lamina. Find the minium periodic time of oscilliation. What is the locus of points about which the periodic time is minimum?
View Solution
Knowledge Check
- Question 1 - Select One
The radius of gyration of a solid sphere of radius r about a certain axis is r. The distance of this axis from the centre of the sphere is
ArB0.5 rC√0.6rD√0.4r - Question 2 - Select One
The radius of gyration of a solid shapere of radius r about a certain axis is r. The distance of this axis from the centre of the shpere is
Aremain stationaryB0.5rC√0.6rD√0.4r - Question 3 - Select One
A disc is made to oscillate about a horizontal axis passing through mid point of its radius. Determine time period.
A2π√3R2gB2π√2R3gC2π√RgD2π√2Rg
An uniform disc is rotating at a constant speed in a vertical plane about a fixed horizontal axis passing through the centre of the disc. A piece of the disc from its rim detaches itself from the disc at the instant when it is at horizontal level with the centre of the disc and moving upwards, then about the fixed axis.
STATEMENT-1 : Angular speed of the disc about the aixs of rotation will increase.
and
STATEMENT-2 : Moment of inertia of the disc is decreased about the axis of rotation.View SolutionA disc of mass M and radius R can rotate freely in a vertical plane about a horizontal axis at O distance r from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information

Reaction force exerted by the hinge on the disc at this instant isView SolutionA disc of mass M and radius R can rotate freely in a vertical plane about a horizontal axis at O distance r from the centre of the disc as shown in Fig. The disc is released from rest in the shown position. Answer the following questions based on the above information
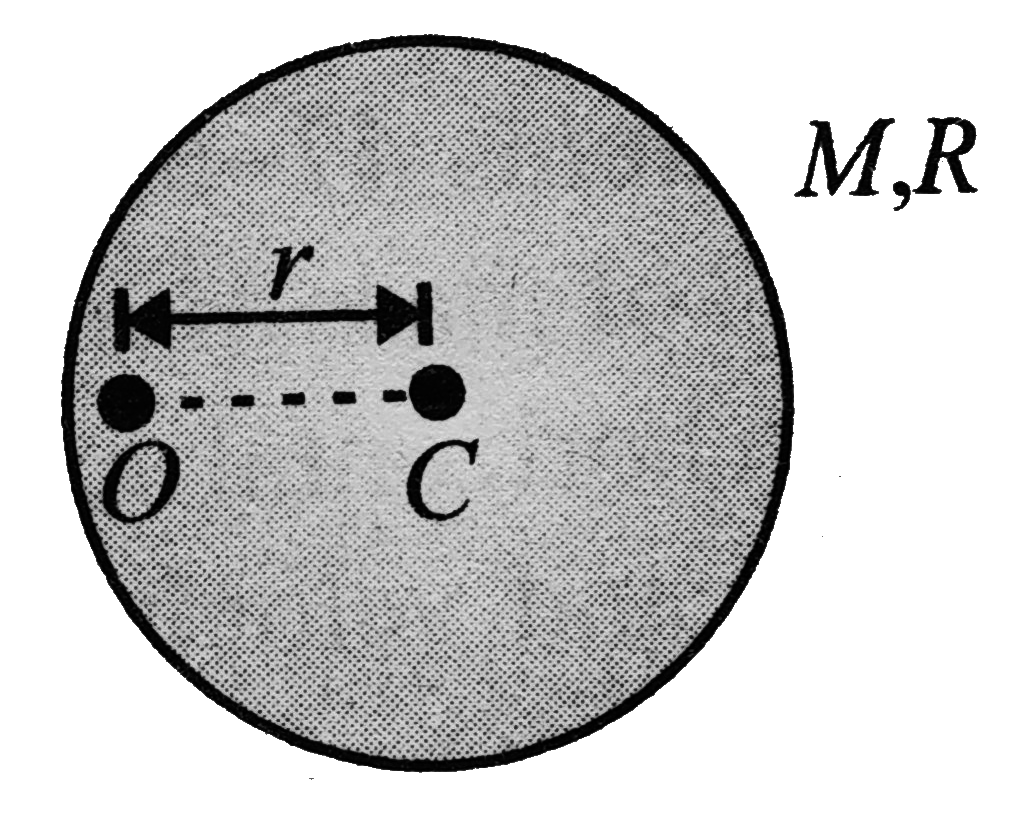
The angular velocity of the disc in the above described case isView SolutionA uniform disc is rotating at a constant speed in a vertical plane about a fixed horizontal axis, passing through the centre of the disc. A piece of disc from its rim detaches itself from the disc at the instant when it is, on the same horizontal with the centre of the disc and moving upwards. lien about the fixed axis, the angular speed of the
View SolutionA uniform disc is rotating at a constantt speed in a vertical plane about a fixed horizontal axis passing through the centre of the disc. A piece of the disc from its rim detaches itself from the disc at the instant when it is at horizontal level with the centre of the disc and moving upward. Then about the fixed axis, the angular speed of the
View Solution

