A thin uniform rod of length l is pivoted at its upper end. It is free to swing in a vertical plane. Its time period for oscillation of small amplitude is
2π√lg
2π√2l3g
2π√3l2g
2π√l3g
The correct Answer is:B
To find the time period of oscillation for a thin uniform rod of length l pivoted at its upper end, we can follow these steps:
Step 1: Understand the System
The rod is pivoted at one end and can swing in a vertical plane. When it swings, it will experience torque due to gravity acting on its center of mass.
Step 2: Identify the Center of Mass
For a uniform rod of length l, the center of mass is located at a distance of l2 from the pivot point.
Step 3: Calculate the Torque
The force acting on the center of mass is the weight of the rod, which is Mg (where M is the mass of the rod and g is the acceleration due to gravity). The torque τ about the pivot point due to this force is given by:
τ=r×F=(l2)×Mg=Mg⋅l2
Step 4: Moment of Inertia
The moment of inertia I of a thin rod about an end is given by:
I=13Ml2
Step 5: Use the Formula for Time Period
The formula for the time period T of a physical pendulum is:
T=2π√Iτ
Substituting the values of I and τ:
T=2π
⎷13Ml2Mg⋅l2
Step 6: Simplify the Expression
Now simplify the expression:
T=2π
⎷13Ml2Mg⋅l2=2π√2l3g
Final Result
Thus, the time period T for small amplitude oscillations of the rod is:
T=2π√2l3g
The rod is pivoted at one end and can swing in a vertical plane. When it swings, it will experience torque due to gravity acting on its center of mass.
For a uniform rod of length l, the center of mass is located at a distance of l2 from the pivot point.
The force acting on the center of mass is the weight of the rod, which is Mg (where M is the mass of the rod and g is the acceleration due to gravity). The torque τ about the pivot point due to this force is given by:
τ=r×F=(l2)×Mg=Mg⋅l2
The moment of inertia I of a thin rod about an end is given by:
I=13Ml2
The formula for the time period T of a physical pendulum is:
T=2π√Iτ
Substituting the values of I and τ:
T=2π
⎷13Ml2Mg⋅l2
Now simplify the expression:
T=2π
⎷13Ml2Mg⋅l2=2π√2l3g
Thus, the time period T for small amplitude oscillations of the rod is:
T=2π√2l3g
Similar Questions
A uniform rod of length l and mass M pivoted about its end as shown in Fig. and is free to rotate in the vertical plane about the pivot. The rod is released from rest in the horizontal position.
(a) What is the initial angular acceleration of the rod?

(b) Find the initial acceleration of the right end of the rod?
( c) Find normal contact force due to hinge when rod has rotated through angle θ as shown in Fig.View SolutionA uniform slender rod of mass M and length L is pivoted at its end. The rod is released from its nearly vertical position. What is the reaction at the pivot when the rod reaches the horizontal position? If the support is withdrawn at this instant, describe the subsequent motion of the rod.
View Solution
Knowledge Check
- Question 1 - Select One
Time period of a simple pendulum of length L is T1 and time period of a uniform rod of the same length L pivoted about an end and oscillating in a vertical plane is T2. Amplitude of osciallations in both the cases is small. Then T1T2 is
A1√3B1C√43D√32 - Question 2 - Select One
Time period of a simple pendulum of length L is T1 and time period of a uniform rod of the same length L pivoted about an end and oscillating in a vertical plane is T2. Amplitude of osciallations in both the cases is small. Then T1T2 is
A√43B1C√32D√13 - Question 3 - Select One
A uniform rod smoothly pivoted at one of its ends is released from rest. If it swings in vertical plane, the maximum speed of the end P of the rod is.
 .A2√3glB√3glC2√2glD√gl
.A2√3glB√3glC2√2glD√gl
A rod of mass m,length l pivoted at its centre is free to rotate in a vertical plane.The rod is at rest and is in vertical position.A bullet of mass m/2 moving horizontally with speed v strikes and sticks to one end of the rod. Angular velocity of system just after collision is
View SolutionTime period of a simple pendulum of length L is T1 and time period of a uniform rod of the same length L pivoted about one end and oscillating in vertical plane is T2. Amplitude of oscillation in both the cased is small. The T1/T2 is:
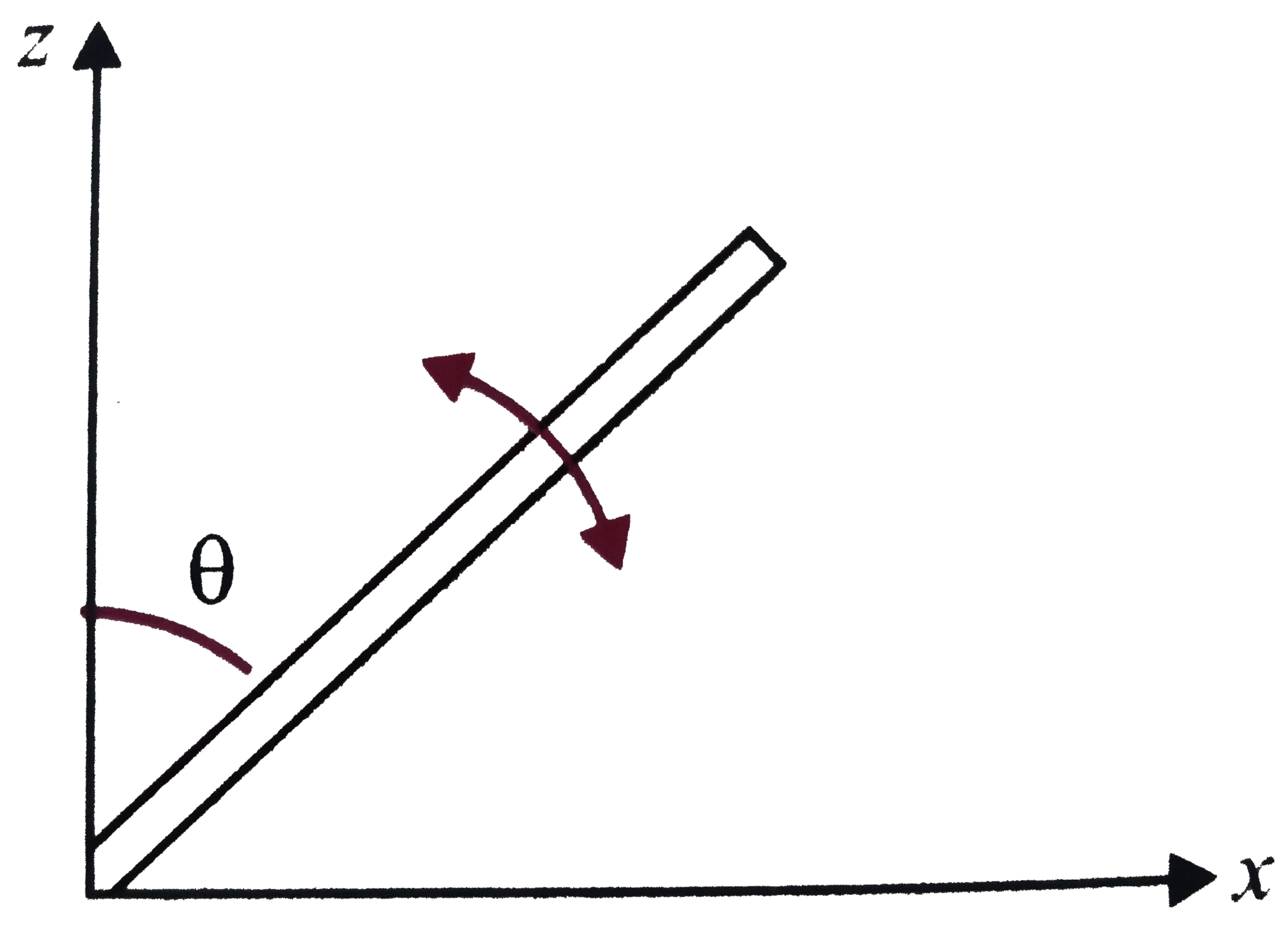
View SolutionA slender uniform rod of mass M and length l is pivoted at one ens so that it can rotate in a vertical plane, Fig. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle θ with the vertical is
 View Solution
View SolutionA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is
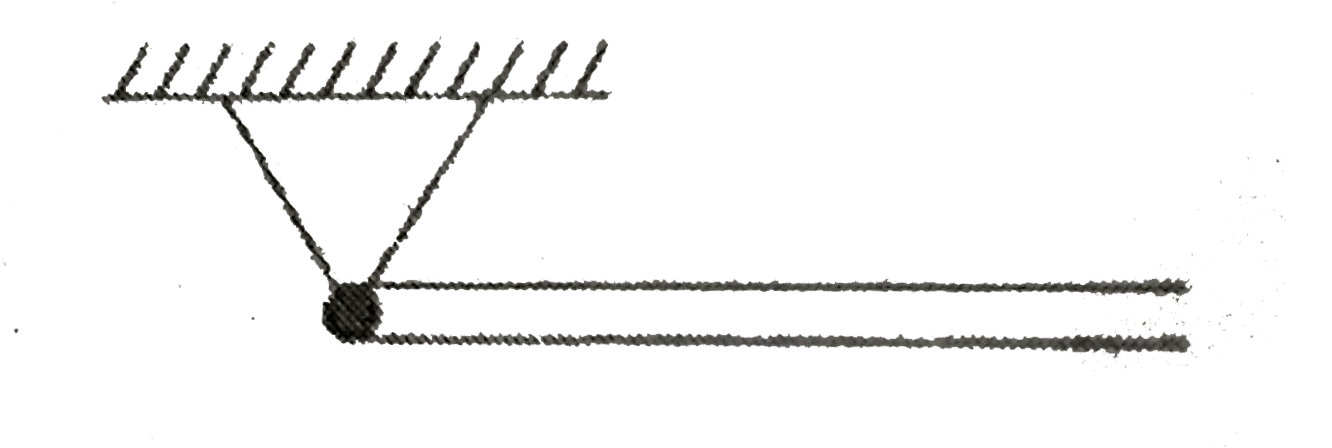 View Solution
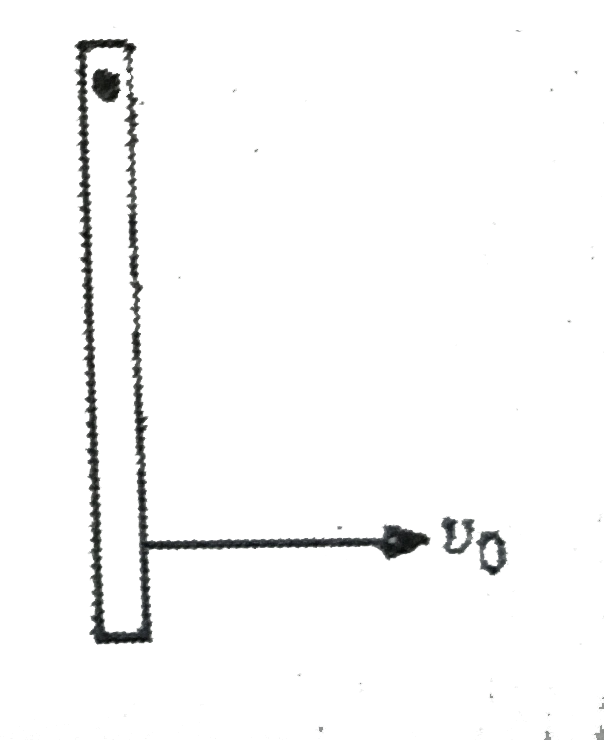
View SolutionA thin uniform rigid rod of length l is hinged at one end so that it can move ina vertical plane by rotating about a horizontal axis through upper end. The lower end is given a sharp blow and made to acquire a linear velocity Maximum height attained by lower end of the rod is:
 View Solution
View Solution

