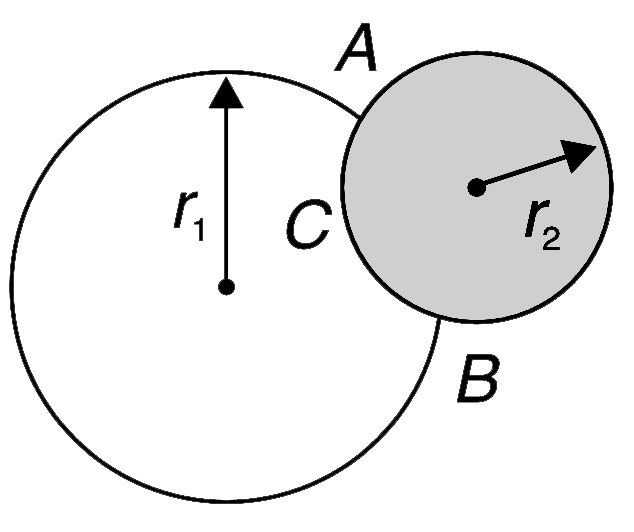
Prove that if two bubbles of radii r1 and r2(r1<r2) come in contact with each other then the radius of curvature of the common surface r=r1r2r2−r1
A
r2−r1
B
r2−r1r1r2
C
r1r2r2−r1
D
r2+r1
Video Solution
Text Solution
The correct Answer is:C
Radius of curvature of common surface is,
RCommon=r1r2r2−r1
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question19videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Match the columns6videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.410videos
FLUID MECHANICS
- BOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective15videos
EXPERIMENTS
- BOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
Similar Questions
Knowledge Check
- Question 1 - Select One
If two bubble of radii 0.03 cm and 0.04 cm come in contact with each other then the radius of curvature of the common surface 'r' is given by.
A0.03B0.06C0.12D0.24 - Question 2 - Select One
Prove that if two bubbles of radii r1 and r2(r1<r2) come in contact with each other then the radius of curvature of the common surface r=r1r2r2−r1
Ar2−r1Br2−r1r1r2Cr1r2r2−r1Dr2+r1 - Question 3 - Select One
Two circles of radii r1 and r2,r1>r2≥2 touch each other externally. If θ be the angle between the direct common tangents, then,
Aθ=sin−1(r1+r2r1−r2)Bθ=2sin−1(r1−r2r1+r2)Cθ=sin−1(r1−r2r1+r2)Dnone of these
Two soap bubble of radius 2r and 3r are in contact with each other. If the radius of curvature of the interface between the bubble in nr then find the value of n:
View SolutionTwo soap bubbles of radius r1 and r2 combine. Find radius of curvature of the common surface separating them.
 View Solution
View SolutionProve that r1+r2+r3−r=4R
View SolutionProve that r1+r2+r3−r=4R
View SolutionTwo soap bubbles of radii r1 and r2 equal to 4 cm and 5 cm are touching each other over a common surface S1S2 (shown in figure). Its radius will be
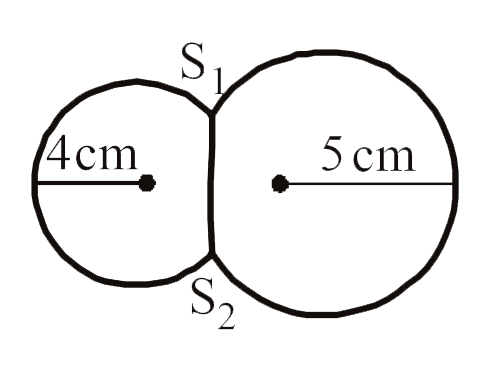 View Solution
View Solution