A metal sphere connected by a string is dipped in a liquid of density ρ as shown in figure. The pressure at the bottom of the vessel will be, (p0=atmospheric pressure )

p=p0=ρgh
p>p0+ρgh
p<p0+ρgh
p0
The correct Answer is:A
Upthrust on sphere form the liquid make equal and opposite pair of forces. Or p=Po+ρgh
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - B) Medical entrance special format question
19 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Match the columns
6 Videos
- FLUID MECHANICSBOOK - DC PANDEYCHAPTER - FLUID MECHANICSEXERCISE - Check point 13.4
10 Videos
- EXPERIMENTSBOOK - DC PANDEYCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
The force F needed to support the liquid of density ρ and the vessel on it, in figure, is
View SolutionA container of cross-section area A resting on a horizontal surface, holds two immiscible and incompressible liquid of densities ρand2ρ as shown in figure. The lower density liquid is open to the atmosphere having pressure P0. The pressure at the bottom of the container is
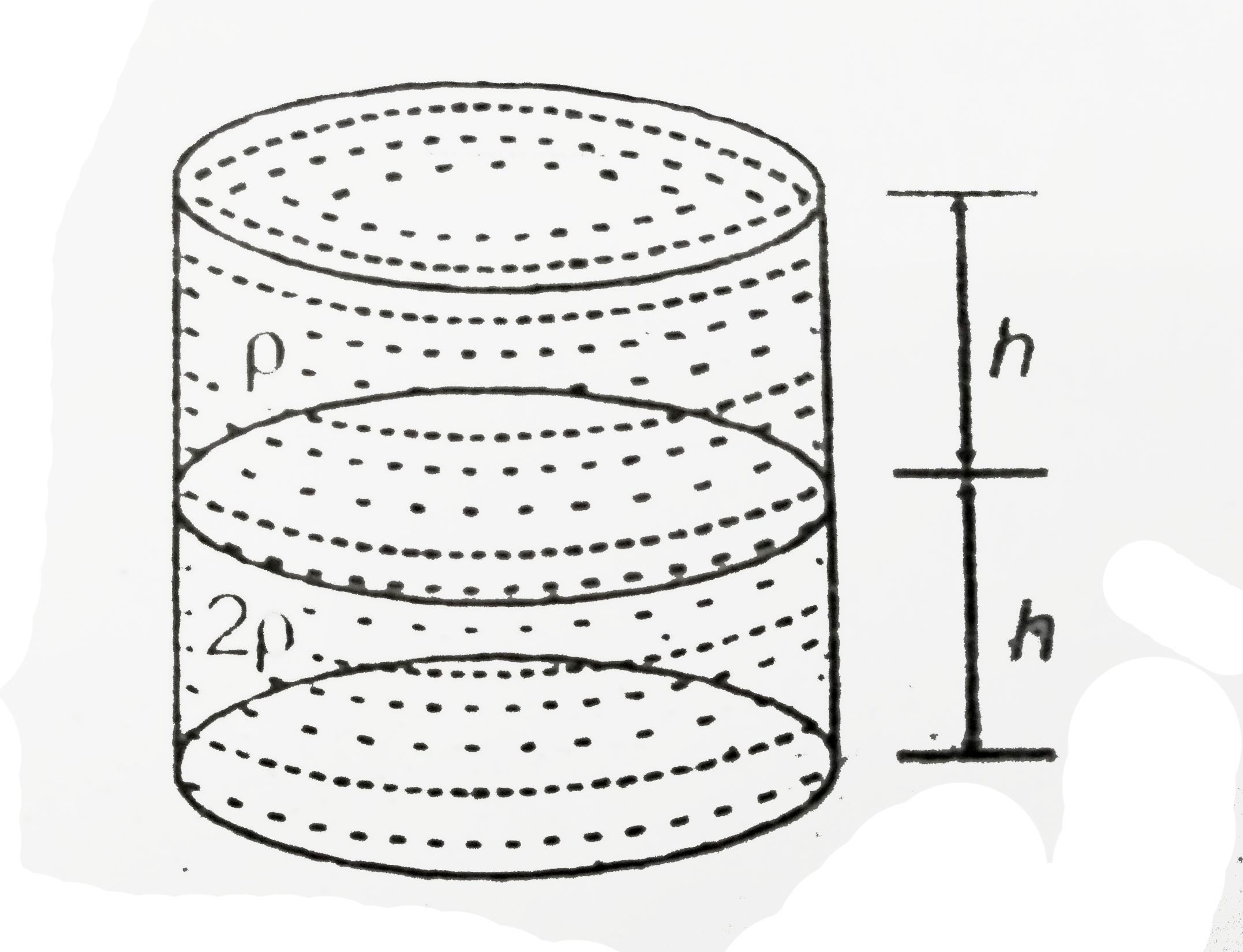
View Solution
Knowledge Check
A rectangular container moves with an acceleration a along the positive direction as shown in figure. The pressure at the A in excess of the atmospheric pressure p0 is (take ρ as the density of liquid)
 AρghBρalCρ(gh+al)DBoth (a) and (b)
AρghBρalCρ(gh+al)DBoth (a) and (b)Figure shows a siphon. Choose the wrong statement.

(p0 = atmospheric pressure)ASiphon works when h>0BPressure at point 2 inside the tube is p2=p0−ρghCPressure at point 3 is p0DNone of the aboveA container shown in figure contains a liquid to depth H, and of density ρ The gauge pressure at point P is :
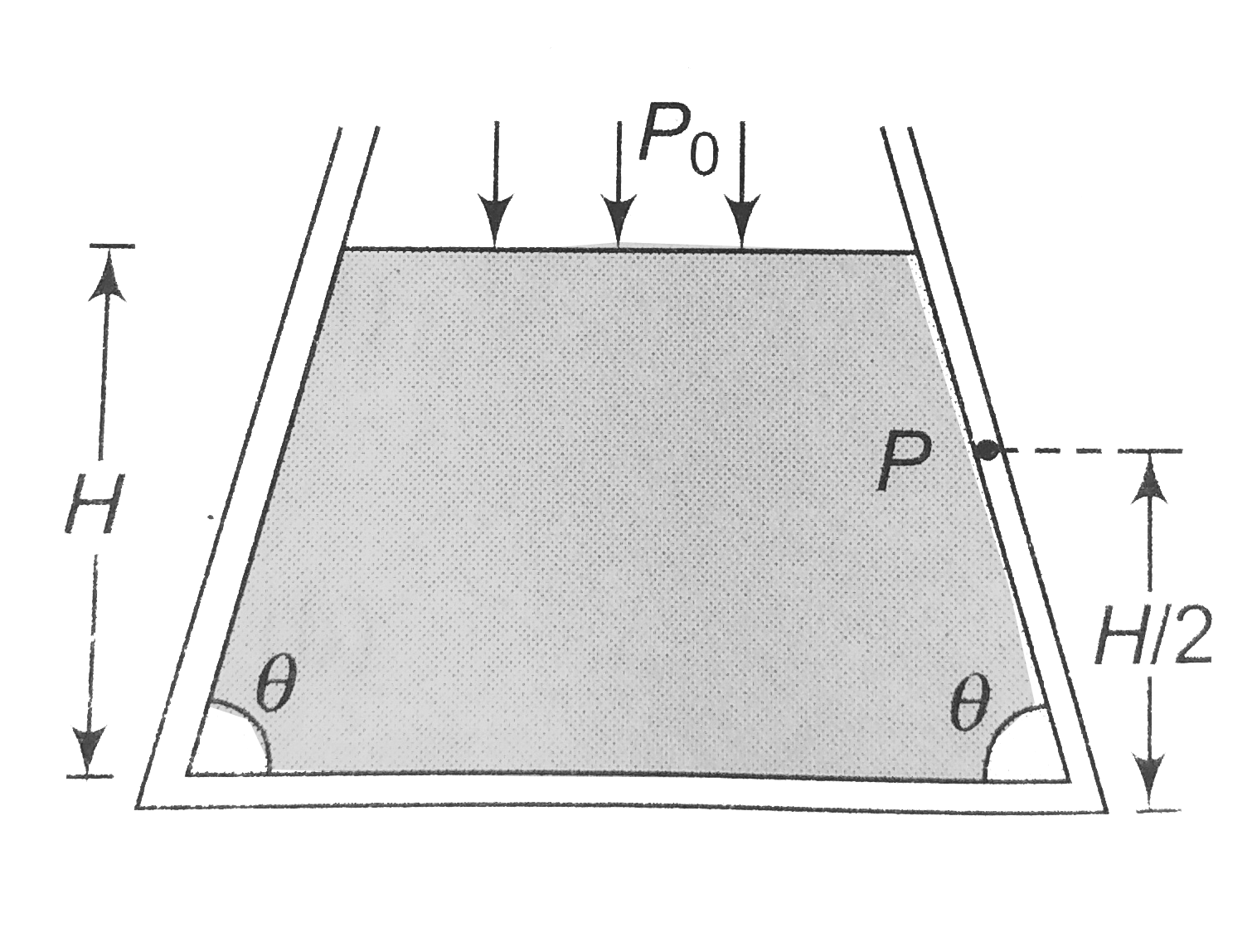 AρgH2+P0BρgH2CρgH2cosθDρgHcosθ2
AρgH2+P0BρgH2CρgH2cosθDρgHcosθ2
A liquid having surface tension T and density ρ is in contact with a vertical solid wall. The liquid surface gets curved as shown in the figure. At the bottom the liquid surface is flat. The atmospheric pressure is Po.
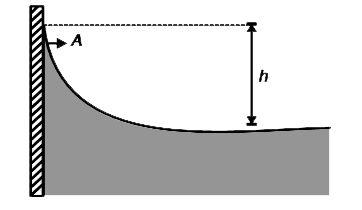
(i) Find the pressure in the liquid at the top of the meniscus (i.e. at A)
(ii) Calculate the difference in height (h) between the bottom and top of the meniscus.
View SolutionA cylidrical vesel containing a liquid is closed by a smooth piston of mass m as shown in the figure. The area of cross section of the piston is A. If the atmospheric pressure is P0, find the pressure of the liquid just below the piston.
 ,
,
View SolutionA tube in vertical plane is shown in figure. It is filled with a liquid of density ρ and its end B is closed. Then the force exerted by the fluid on the tube at end B will be : [Neglect atmospheric pressure and assume the radius of the tube to be negligible in comparison to l]

View SolutionLiquid of density ρ in a container exerts pressure P given by (height of liquid h and area A)
View SolutionA cylinder of mass m and density ρ hanging from a string is lowered into a vessel of cross-section area s containing a liquid of density σ(<ρ) unit it is fully immersed. The increase in pressure at the bottom of the vessel is
View Solution
