A uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate dBdt. Loop 1 of radius R > r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
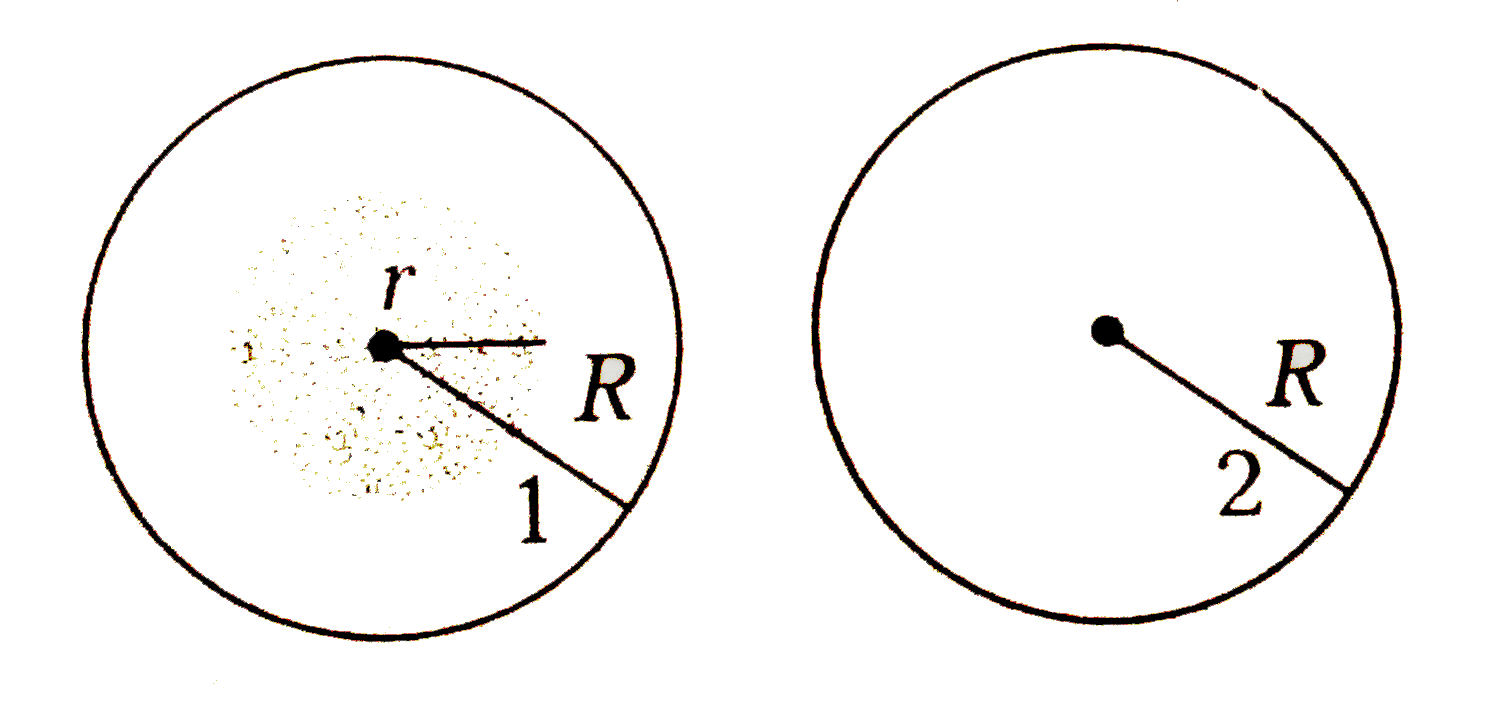
Zero in loop 1 and zero in loop 2
−dBdtπr2 in loop 1 and −dBdtπ2 in loop 2
−dBdtπR2 in loop 1 and zero in loop 2
−dBdtπr2 in loop 1 and zero in loop 2
The correct Answer is:C
Induced emf in the region is given by
|e|=dhπdt
where, ϕ=BA=πr2B
⇒ dϕ1dt−πr2dBdt
Rate of change if magnetic flux associated with loop l,
e1=−dϕ1dt=−πr2dBdt
Similarly, e2 = emf associated with loop 2
=−dϕ2dt=0 (∵ϕ2=0)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Match the columns
5 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A uniform magnetic field is restricted within a region of radius 1m. The magnetic field changes with time(t) as →B=B0(2t3)ˆk. A loop of radius 2m is outside the region of magnetic field as shown in figure. The emf induced in loop is
_PHY_E06_055_Q01.png)
View SolutionA current carrying loop of radius R and mass 'm' is placed inside a uniform magnetic field an shown

View Solution
Knowledge Check
A uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate dBdt. Loop 1 of radius R > r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
 A−d→BdtπR2 in loop 1 and zero in loop 2B−d→Bdtπr2 in loop 1 and zero in loop 2CZero in loop 1 and zero in loop 2D−d→Bdtπr2 in loop 1 and −d→Bdtπr2 in loop 2
A−d→BdtπR2 in loop 1 and zero in loop 2B−d→Bdtπr2 in loop 1 and zero in loop 2CZero in loop 1 and zero in loop 2D−d→Bdtπr2 in loop 1 and −d→Bdtπr2 in loop 2The magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate.dBdt . Then
Athe emf induced in the ring is πr2dBdtBthe emf induced in the ring is 2πrdBdtCdiametrically opposite points on the ring are at the same potentialDall points on the ring are at the same potentialA uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the loop and the magnitude of field is increasing at a constant rate α. There is a straight conducting rod of length 2R placed as shown in figure.
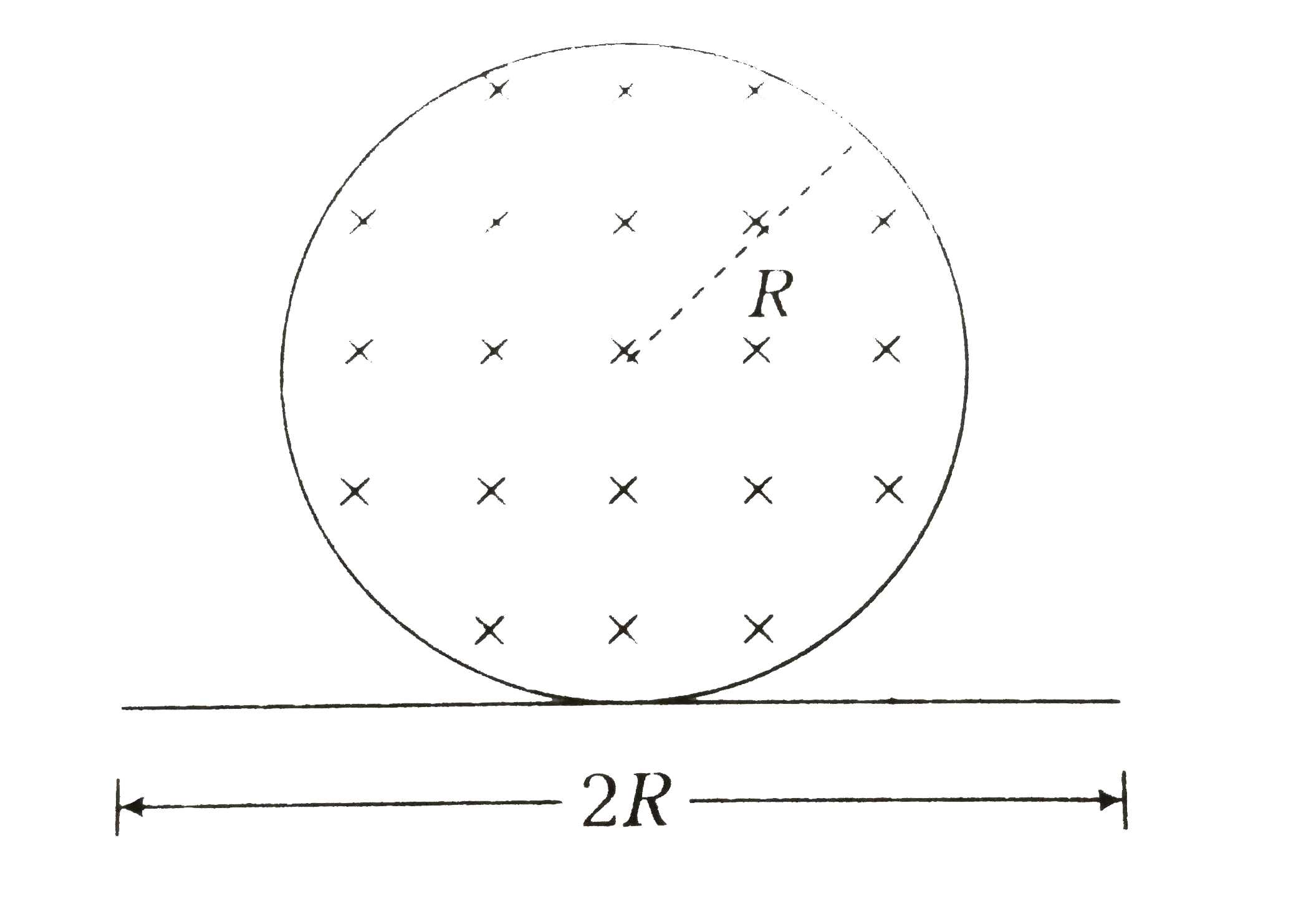
The magnitude of induced emf across the rod isAπR2αBπR2α2CR2α√2Dπr2α4
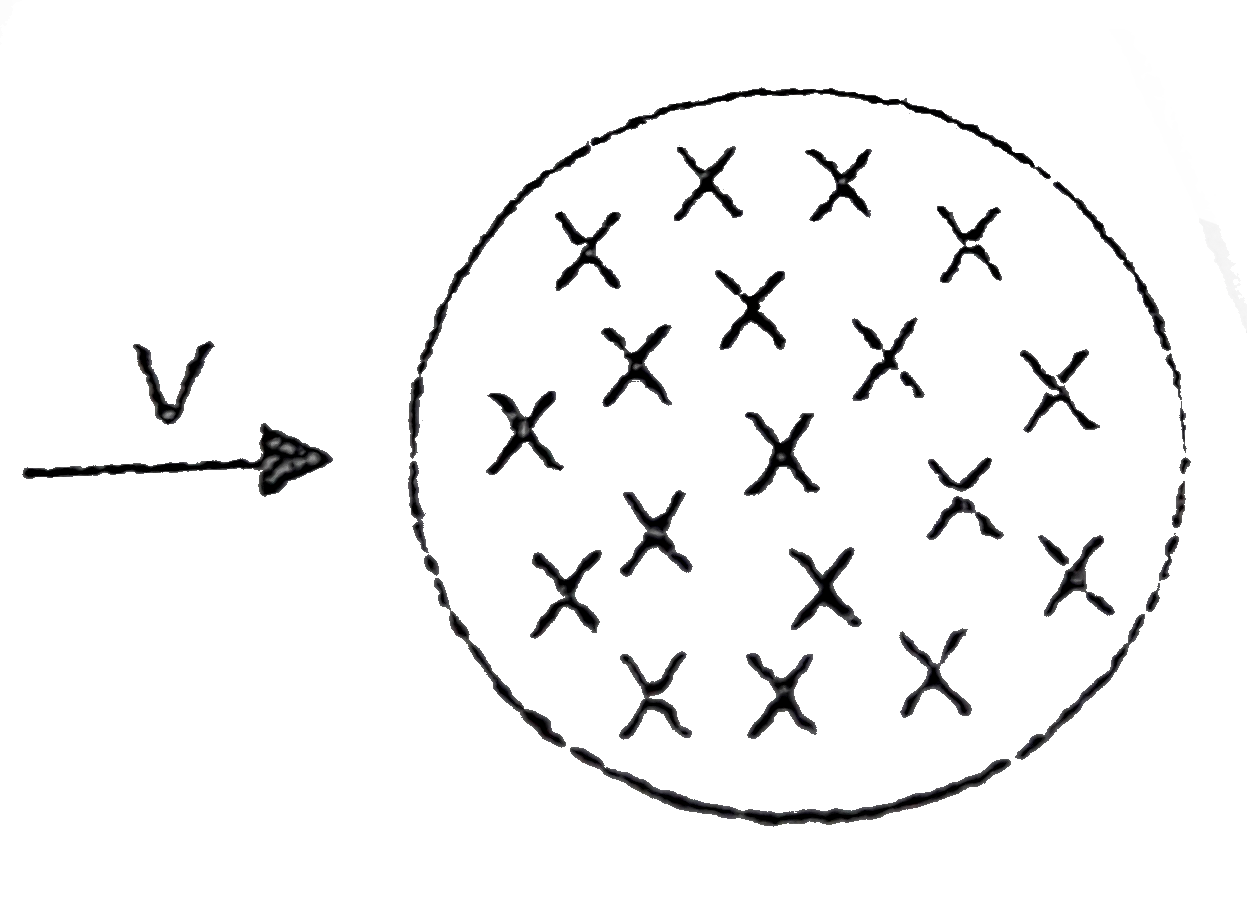
A uniform magnetic field exists in a circular region of radius r.The magnitude of magnetic field is B and points inward.An electron flies into the region radially as shown in figure.After a certain time, the electron deflected by the magnetic field leaves the region.The time interval during which the electron moves in the region is Nmtan−1eBrmVeB.Then find value of N.(m is mass of electron and e is charge of electron)
View SolutionA uniform magnetic field B exists in a circular region of radius R. the field is perpendicular to the plane and is increasing at a constant rate of dBdt=α. There is a straight conducing rod AB of length 2R. Find the emf induced in the rod when it is placed as shown in figure (a) & (b). Point C is midpoint of the rod in figure (b)

View SolutionMagnetic field in cylindrical region of radius R in inward direction is as shown in figure.
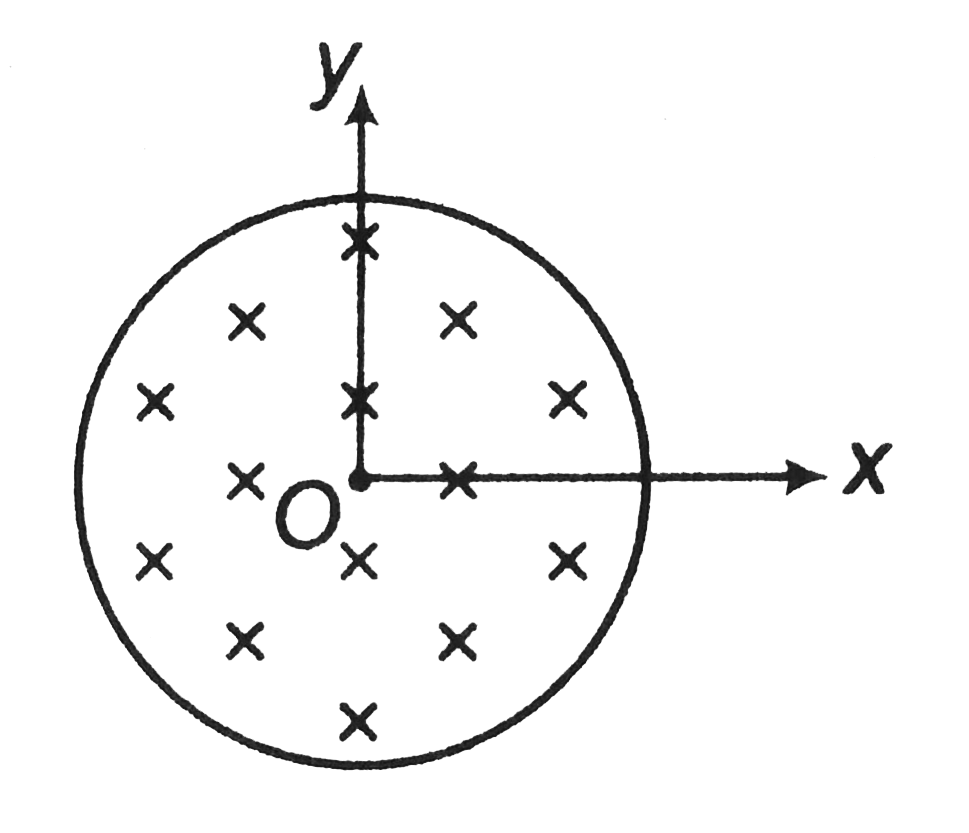
View SolutionA uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the loop and the magnitude of field is increasing at a constant rate α. There is a straight conducting rod of length 2R placed as shown in figure.

The magnitude of induced emf across the rod is
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r change ate the rate dBdt
View Solution
