When an AC voltage, of variable frequency is applied to series L-C-R circuit , the current in the circuit is the same at 4 kHz and 9 kHz. The current in the circuit is maximum at
5 kHz
6.5 kHz
4.2 kHz
6 kHz
The correct Answer is:D
To solve the problem step by step, we will analyze the given information about the series L-C-R circuit and the conditions under which the current is the same at two different frequencies.
1. Understanding the Given Information:
We know that the current in the circuit is the same at two different frequencies: f1=4kHz and f2=9kHz.
2. Using the Relationship of Current in an L-C-R Circuit:
In a series L-C-R circuit, the current I can be expressed as:
I=VZ
where Z is the impedance of the circuit. The impedance Z is given by:
Z=√R2+(XL−XC)2
where XL=ωL (inductive reactance) and XC=1ωC (capacitive reactance).
3. Setting Up the Condition for Equal Currents:
Since the current is the same at both frequencies, we can write:
Z1=Z2
This implies:
√R2+(XL1−XC1)2=√R2+(XL2−XC2)2
4. Expressing Reactances in Terms of Frequencies:
We can express the reactances at the two frequencies:
- For f1=4kHz:
XL1=2πf1L,XC1=12πf1C
- For f2=9kHz:
XL2=2πf2L,XC2=12πf2C
5. Equating the Impedance Conditions:
From the condition Z1=Z2, we can derive:
(XL1−XC1)2=(XL2−XC2)2
This leads to two possible cases:
XL1−XC1=XL2−XC2orXL1−XC1=−(XL2−XC2)
6. Finding the Resonant Frequency:
The maximum current occurs at the resonant frequency fr, where:
XL=XC
This gives:
2πfrL=12πfrC
Rearranging gives:
fr=12π√LC
7. Calculating the Resonant Frequency:
We know that the product of the two frequencies where the current is the same can be used to find the resonant frequency:
fr=√f1⋅f2=√4kHz⋅9kHz=√36kHz=6kHz
Final Answer:
The current in the circuit is maximum at 6 kHz.
---
We know that the current in the circuit is the same at two different frequencies: f1=4kHz and f2=9kHz.
In a series L-C-R circuit, the current I can be expressed as:
I=VZ
where Z is the impedance of the circuit. The impedance Z is given by:
Z=√R2+(XL−XC)2
where XL=ωL (inductive reactance) and XC=1ωC (capacitive reactance).
Since the current is the same at both frequencies, we can write:
Z1=Z2
This implies:
√R2+(XL1−XC1)2=√R2+(XL2−XC2)2
We can express the reactances at the two frequencies:
- For f1=4kHz:
XL1=2πf1L,XC1=12πf1C
- For f2=9kHz:
XL2=2πf2L,XC2=12πf2C
From the condition Z1=Z2, we can derive:
(XL1−XC1)2=(XL2−XC2)2
This leads to two possible cases:
XL1−XC1=XL2−XC2orXL1−XC1=−(XL2−XC2)
The maximum current occurs at the resonant frequency fr, where:
XL=XC
This gives:
2πfrL=12πfrC
Rearranging gives:
fr=12π√LC
We know that the product of the two frequencies where the current is the same can be used to find the resonant frequency:
fr=√f1⋅f2=√4kHz⋅9kHz=√36kHz=6kHz
The current in the circuit is maximum at 6 kHz.
Similar Questions
When an AC voltage, of variable frequency is applied to series L-C-R circuit, the current in the cirucit is the same at 4kHz. The current in the ciruit is maximum at (x)kHz. Find the value of x
View SolutionAn alternating voltage of frequency f is applied across a series LCR circuit.Le fr be the resonance frequency for the circuit.Will the current in the circuit lag, lead or remain in phase with the applied voltage when (i)f>fr,(ii)f<fr ? Explain your answer in each case.
View Solution
Knowledge Check
In LCR series AC circuit, the current
Ais always in phase with voltageBalways lags behind the generator voltageCalways leads the generator voltageDmay be in phase, lag behind or lead by the generator voltage depending on the values of L,C and RIn an LCR series ac circuit, the current is
Aalways in phase with the voltageBlags the generator voltageCleads the generator voltageDnone of theseThe current in the series L-C-R circuit is
Ai=imsin(ωt+ϕ)Bi=vm√R2+(Xc−XL)2sin(ωt+ϕ)Ci=2imcos(ωt+ϕ)DBoth (a) and (b)
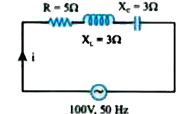
A series L-C-R circuit is given in figure . The current through the circuit is
View SolutionIn an ac circuit, the current lags behind the voltage by π/3. The components in the circuit are
View SolutionIn a series L-C-R circuit shown in the figure , what is the resonance frequency and the current at the resonating frequency?
View SolutionIn an electrical circuit R,L,C and an AC voltage source are all connected in series. When L is removed from the circuit, the phase difference between the voltage and the current in the circuit is π/3. If instead, C is removed from the circuit, difference the phase difference is again π/3. The factor of the circuit is
View SolutionWhen a capacitance is connected in series with a series L-R, a.c. circuit, the total impedance of the circuit
View Solution