An inductor $X_{L}$ = 2 $Ω$ ) , a capacitor ( $X_{C}$ = 8 $Ω$ ) and a resistance (R = 8 $Ω$ ) are connected in series with an AC source . The voltage output of AC source is given by V = 10 cos(100 $π$ t)
The instantaneous potential difference between points A and B, when the applied voltage is 3/5th of the maximum value of applied voltage is

A

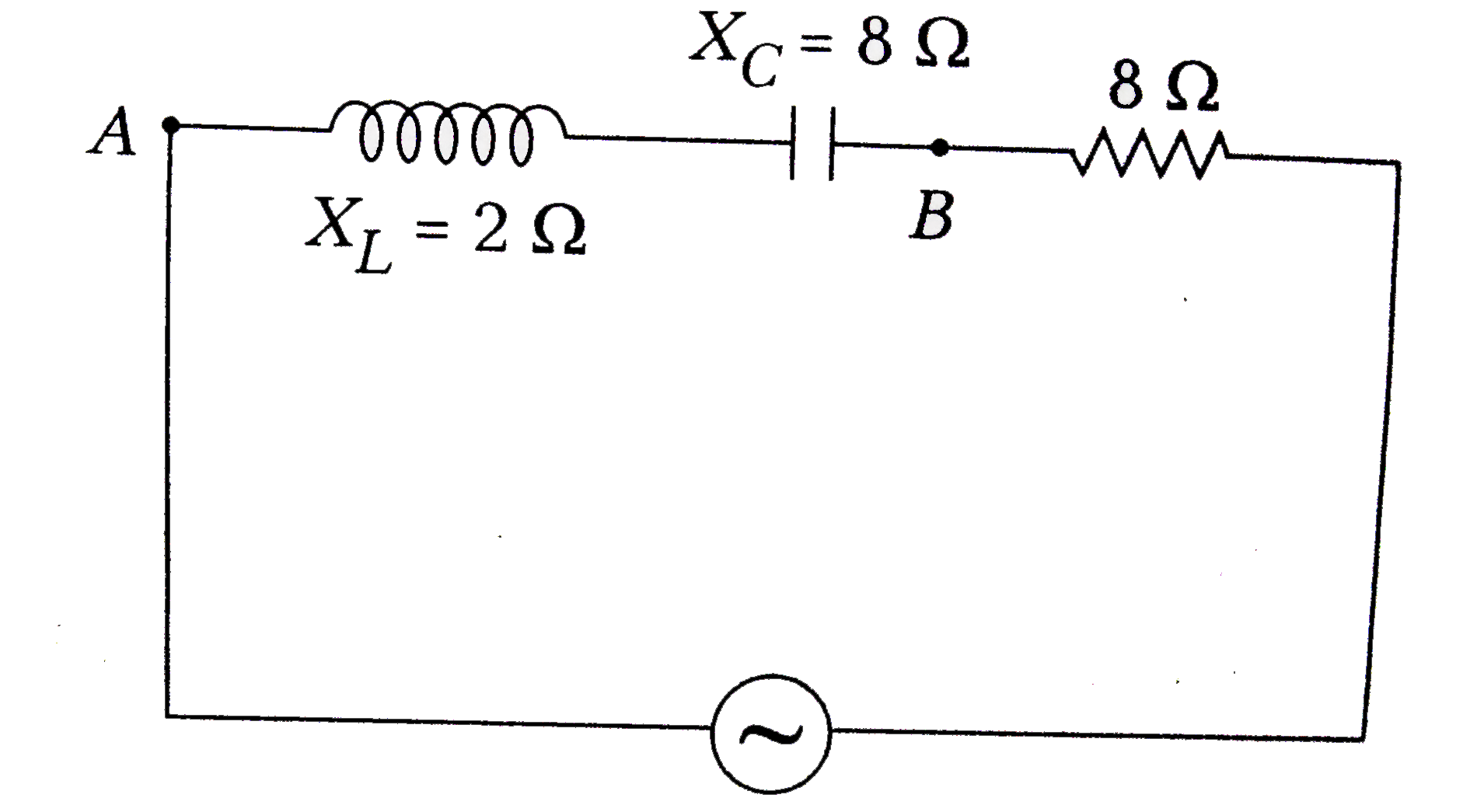
0 V

B

6 V

C

8 V

D

None of these

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Z = $\sqrt{R^{2} + {(X_{C} - X_{L})}^{2}} = 10 Ω$
cos $ϕ = \frac{R}{Z} = \frac{4}{5}$
$∴ ϕ = 37^{\circ}$
$I_{0} = \frac{V_{0}}{Z} = \frac{10}{10} = 1 A$
$I = 1 \cos (100 π t + 37^{\circ})$
$V = 10 \cos (100 π t)$
The applied voltage is $\frac{3}{5}$ th of the maximum applied voltage when , or $100 π t = 53^{\circ}$
$∴ I = 1 \cos (53^{\circ} + 37^{\circ}) = 0$
$∴ V_{A} B = V_{applied} = \frac{3}{5} \times 10 = 6 V$

|

Updated on:21/07/2023

Class 12 PHYSICS ALTERNATING CURRENT

Similar Questions

Knowledge Check

Question 1 - Select One
An inductor $(X_{L} = 2 Ω)$ a capacitor $(X_{C} = 8 Ω)$ and a resistance $(8 Ω)$ are connected in series with an ac source. The voltage output of $A . C$ source is given by $v = 10 cos 100 π t$ . The instantaneous p.d. between $A$ and $B$ when is half of the voltage output from source will be:

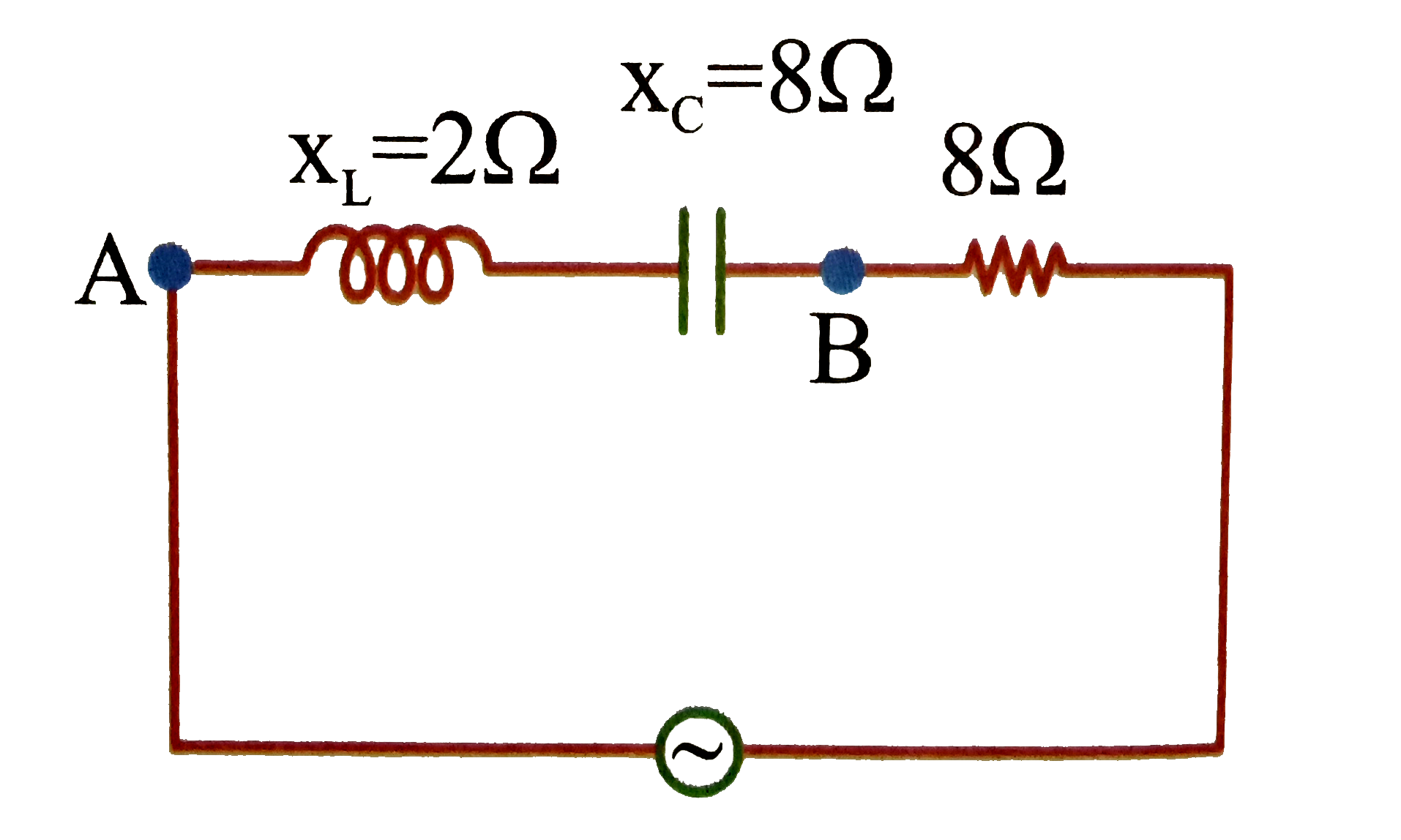A $\frac{24}{7}$ volt
B $\frac{24}{5}$ volt
C $\frac{7}{24}$ volts
D $\frac{5}{24}$ volts
Question 2 - Select One
An inductor $(L = \frac{1}{100 π} H)$ , a capacitor $(C = \frac{1}{500 π} F)$ and a resistance $(3 Ω)$ is connected in series with an AC voltage source as shown in the figure. The voltage of the AC source is given as $V = 10 cos (100 π t)$ volt. What will be the potential difference between A and B ?

A $8 cos (100 π t - 127^{\circ})$ volt
B $8 cos (100 π t - 53^{\circ})$ volt
C $8 cos (100 π t - 37^{\circ})$ volt
D $8 cos (100 π t + 37^{\circ})$ volt
Question 3 - Select One
A $100 Ω$ resistance is connected in series with a $4 H$ inductor. The voltage across the resistor is $V_{R} = 2 sin (1000 t) V$ . The voltage across the inductors is
A $80 sin (1000 t + \frac{π}{2})$
B $40 sin (1000 t + \frac{π}{2})$
C $80 sin (1000 t - \frac{π}{2})$
D $40 sin (1000 π - \frac{π}{2})$

Recommended Questions

Home
Ask Doubt
Profile