Kinetic energy of electron in nth orbit is given by

A

$\frac{R h c}{2 n^{2}}$

B

$\frac{2 R h c}{n}$

C

$\frac{R h c}{n}$

D

$\frac{R h c}{n^{2}}$

Text Solution

Verified by Experts

The correct Answer is:D

Updated on:21/07/2023

|

Class 12 PHYSICS ATOMS

Topper's Solved these Questions

Similar Questions

$r_{n, z} =$ Radius of nth orbit of a single electron species having atomic number 'z'
$u_{n, z} =$ Velocity of electron in nth orbit of a single electron specie having atomic number 'z'
$E_{n, z} =$ Magnitude of total energy of electron in nth orbit of a single electron species having atomic number 'z'.
$K_{n, z} =$ Magnitude of kinetic energy of electron in nth orbit of a single electron species having atomic number 'z'
$P_{n, z} =$ Magnitude of potential energy of electron in nth orbit of a single electron species having atomic number 'z'
$f_{n, z} =$ Frequency of electron in nth orbit of a single electron species having atomic number 'z'.
$T_{n, z} =$ Time period of electron in nth orbit of a single electron species having atomic number 'z'

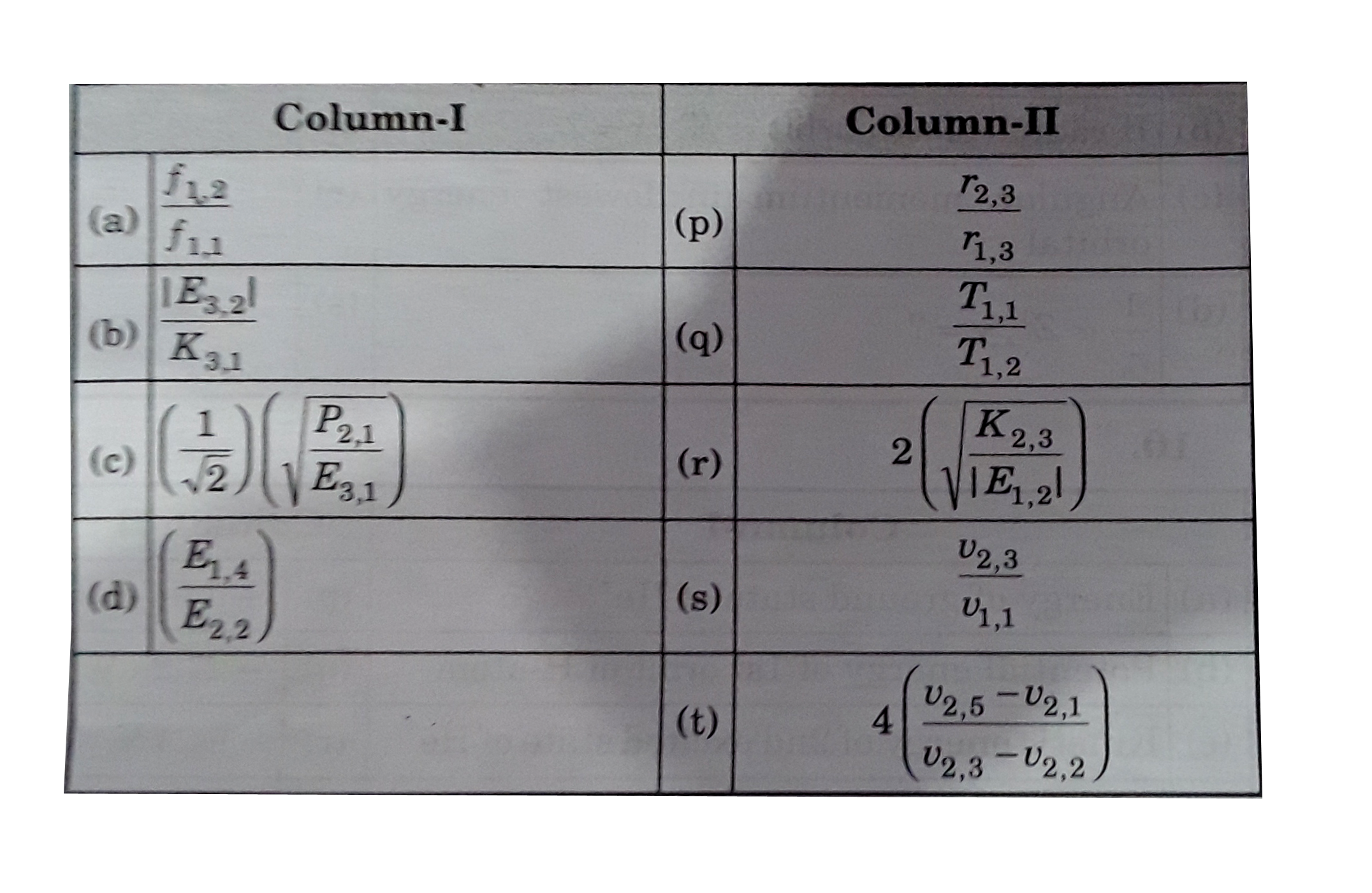
View Solution
Kinetic energy of electron in $n^{th}$ orbit in H-atom
View Solution

Knowledge Check

The angular momentum of electron in nth orbit is given by
A $n h$
B $\frac{h}{2 π n}$
C $n \frac{h}{2 π}$
D $n^{2} \frac{h}{2 π}$
The kinetic energy of the electron in the nth orbit of an atom is given by the relation
A $- \frac{4 π^{2} m e^{4}}{n^{2} h^{2}}$
B $- \frac{2 π^{2} m e^{4}}{n^{2} h^{2}}$
C $- \frac{2 π^{2} m e^{4}}{n^{2} h^{2}}$
DNone of these
Potential energy $(P E_{n})$ and kinetic energy $(K E_{n})$ of electron in nth orbit are related as
A $P E_{n} = K E_{n}$
B $P E_{n} = - 2 K E_{n}$
C $P E_{n} = 2 K E_{n}$
D $P E_{n} = K E_{n}$

DC PANDEY-ATOMS-Check point 12.2

Home
Ask Doubt
Profile