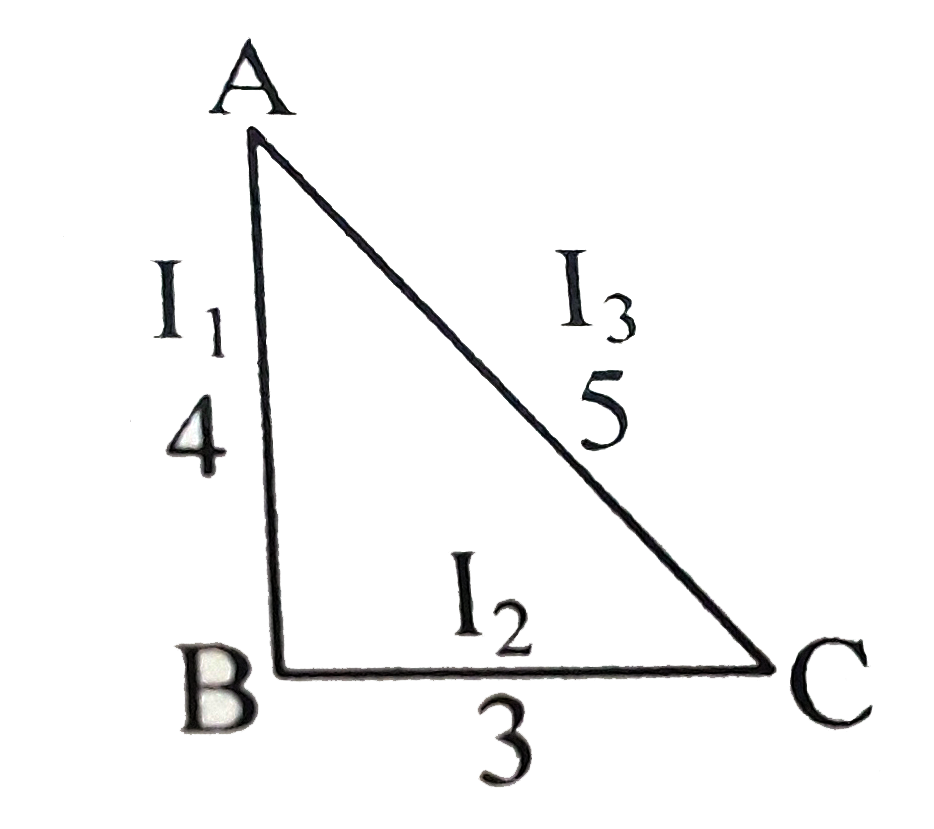
ABC is right angled triangular plane of uniform thickness The sides are such that AB gt BC as sshown in figure I1,I2,I3 are moments of inertia about AB, BC and AC, respectively.Then which of the following relations is correct?
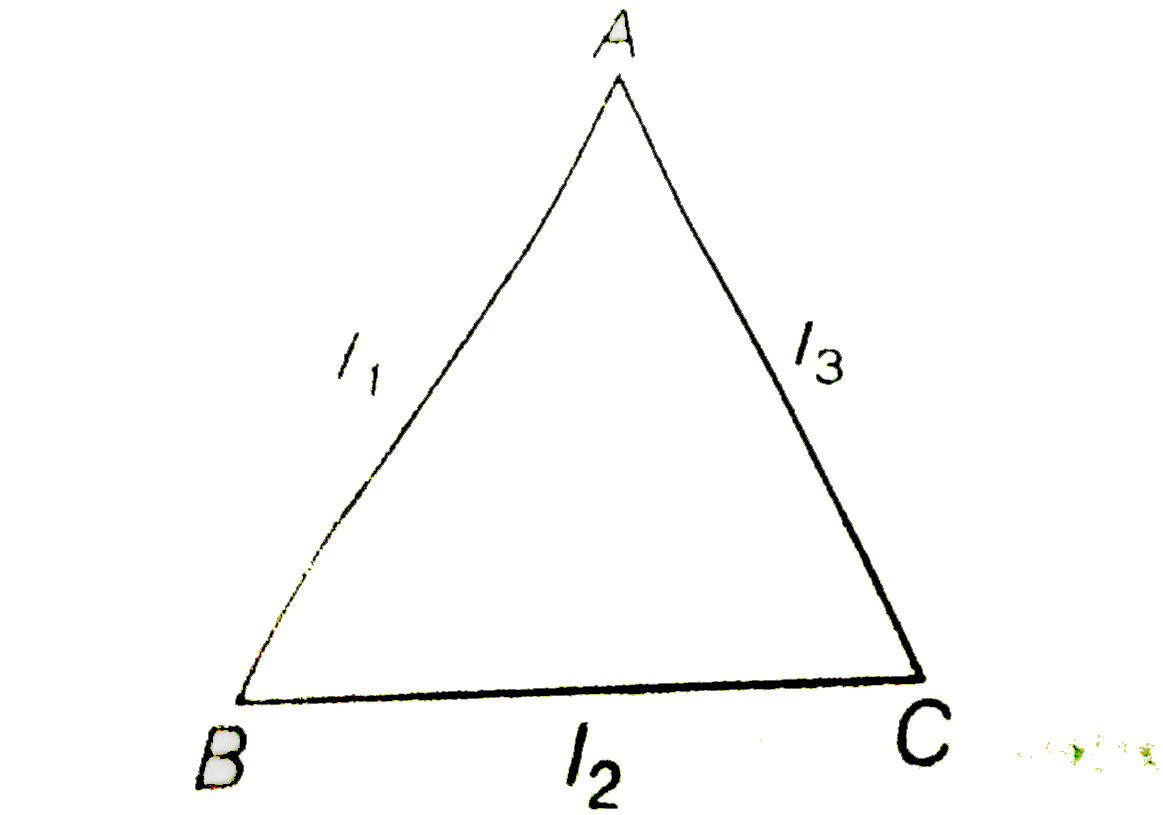
l1=I2=l3
l2>l1>l3
l3<l2<l1
l3>l1>l2
The correct Answer is:b
The moment of inertia of a body about an axis depends not onluy on the mass of the body but also on the distribution of mass about the axis . Fo a given body mass is same so it will depend only on the distribution of mass about the axis .The mass is farthest from axis BC,So I2 is maximum mass is nearest to axis AC, so I3 is minimum.
Hence the correct sequence will be I2>I1>I3
Topper's Solved these Questions
Similar Questions
ABC is a triangular plate of uniform A thickness. The sides are in the ratio shown in the figure. IAB,IBC,ICA are the moments of inertia of the plated about AB,BC and CA respectively. Which one of the following relation is correct?
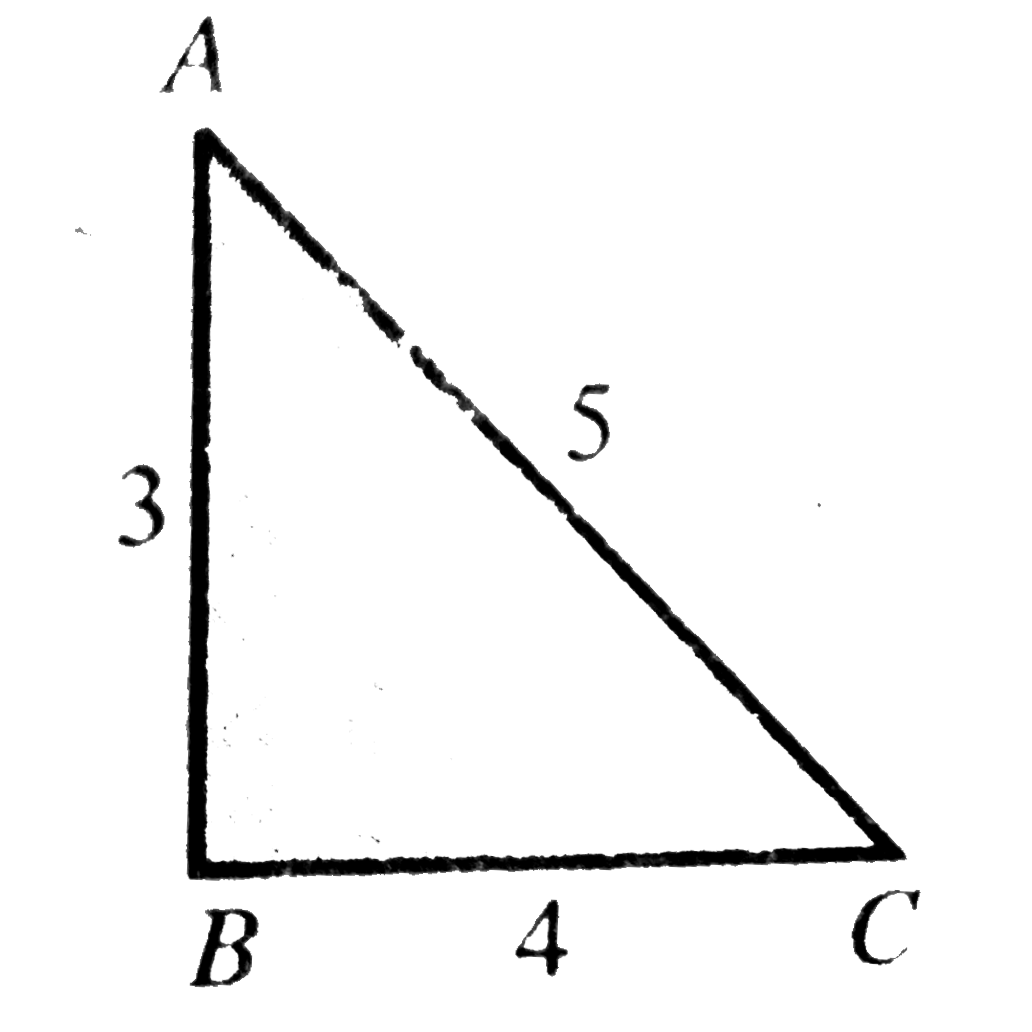
View SolutionABC is a traiangular plate of uniform thickness. The sides are in the ratio shown in the figure. IAB, IBC and ICA are the moments of inertia of the plate about AB, BC and CA repectively. Which one of the following relations is correct?
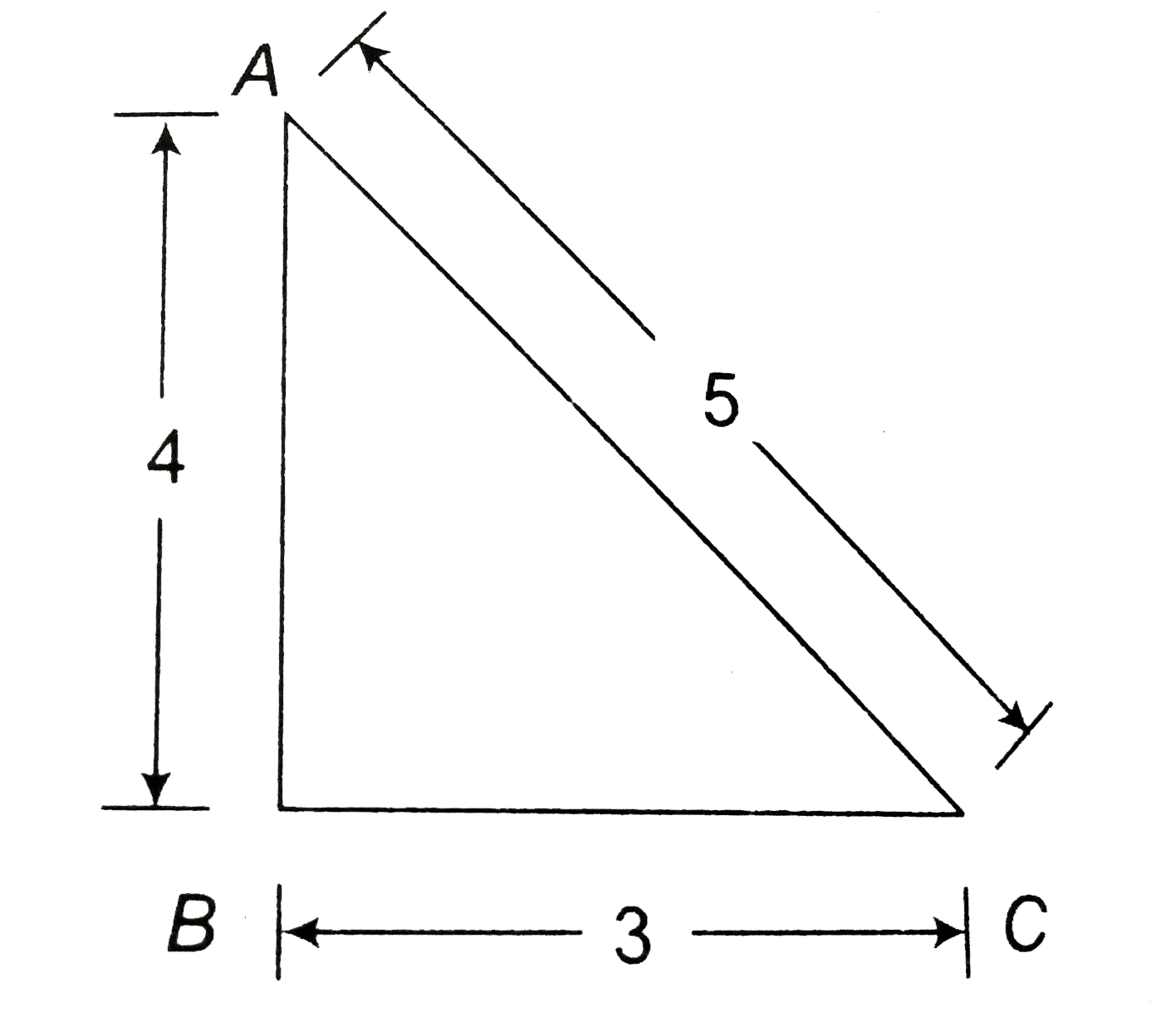
View Solution
Knowledge Check
ABC is a right angled triangular plate of uniform thickness. The sides are such that AB>BC as shown in figure. I1,I2,I3 are moments of inertia about AB,BC and AC respectively. Then which of the following relations is correct?
 AI1=I2=I3BI2>I1>I3CI3<I2<I1DI3>I1>I2
AI1=I2=I3BI2>I1>I3CI3<I2<I1DI3>I1>I2ABC is a right angled triangular plate of uniform thickness. The sides are such that AB>BC as shown in figure. I1,I2andI3 are moments of inertia about AB,BC and AC respectively. Then, which of the following relation is correct ?
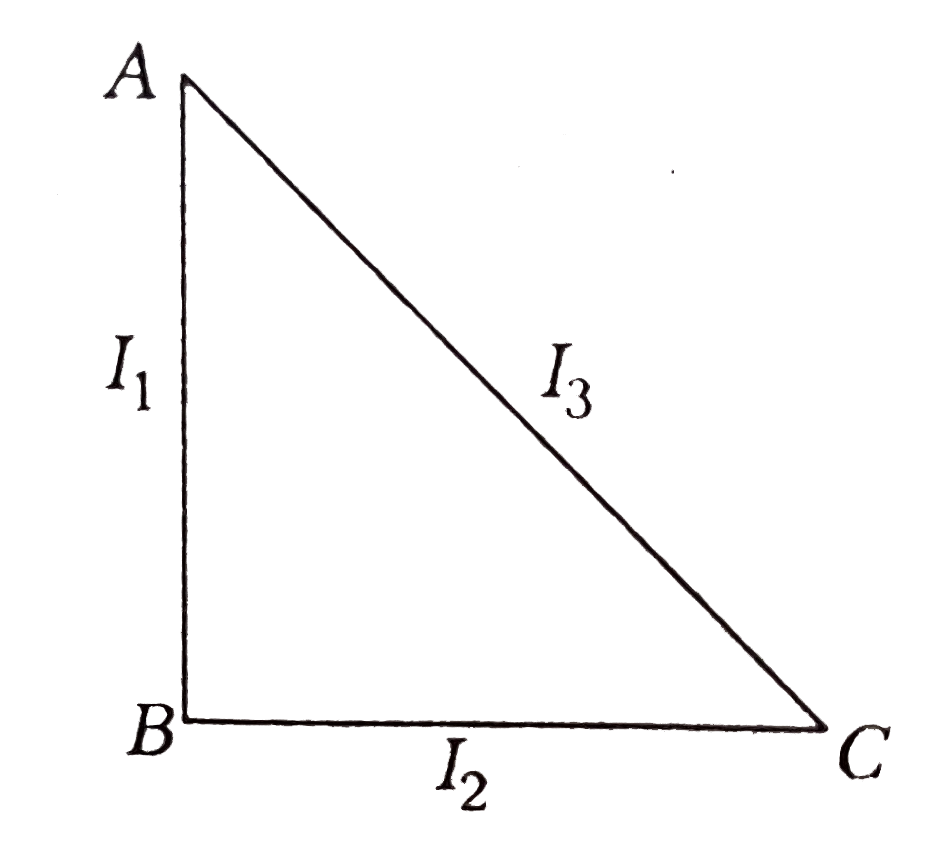 AI1=I2=I3BI2>I1>I3CI3<I2<I1DI2>I1>I2
AI1=I2=I3BI2>I1>I3CI3<I2<I1DI2>I1>I2ABC is a triangular plate of uniform A thickness. The sides are in the ratio shown in the figure. IAB,IBC,ICA are the moments of inertia of the plated about AB,BC and CA respectively. Which one of the following relation is correct?
 AICA is maximumBIAB>IBCCIBC>IABDIAB+IBC=ICA
AICA is maximumBIAB>IBCCIBC>IABDIAB+IBC=ICA
In ΔABC, C is right angle and a perpendicular 'p' is drawn on side AB. If a, b, c are length of sides BC, CA, AB respectively then which of the following is correct?
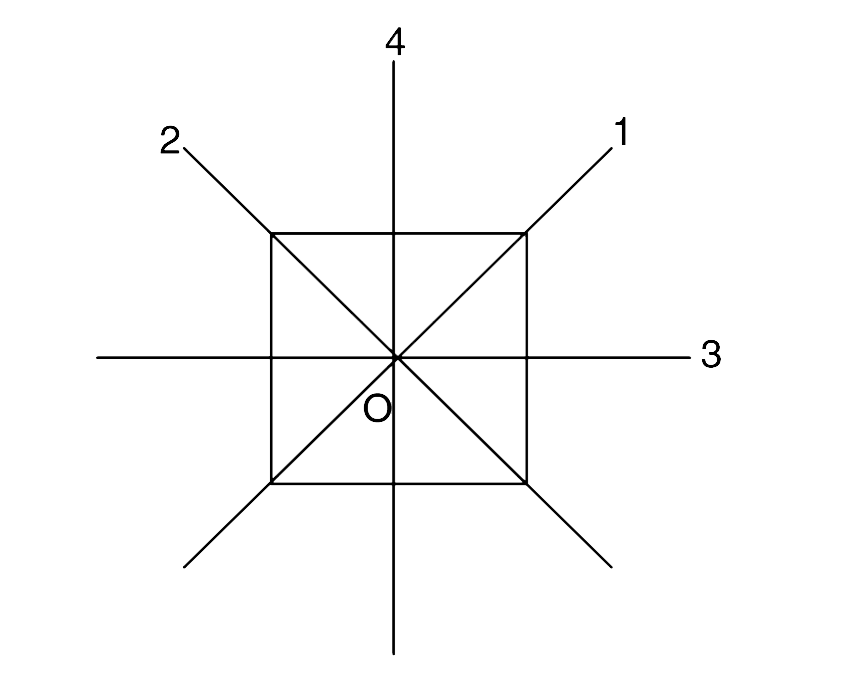
View SolutionConsider a uniform square plate shown in the figure. I1,I2,I3 and I4 are moment of inertia of the plate about the axes 1, 2, 3 and 4 respectively. Axes 1 and 2 are diagonals and 3 and 4 are lines passing through centre parallel to sides of the square. The moment of inertia of the plate about an axis passing through centre and perpendicular to the plane of the figure is equal to which of the followings.
(a) I3+I4
(b) I1+I3
(c) I2+I3
(d) 12(I1+I2+I3+I4)
View SolutionFor the adjoining diagram, a triangular lamina is shown the correct relation between I1,I2 & I3 is (I - moment of inertia)
View SolutionThe ABC is a triangular plate of uniform thickness. The sides are in the ratio shown in the figure. IAB,IBC and lCA are the moments of inertia of the plate about AB, BC and CA respectively. Which one of the following relation is correct?
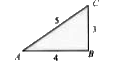
View SolutionABC is a traiangular plate of uniform thickness. The sides are in the ratio shown in the figure. IAB, IBC and ICA are the moments of inertia of the plate about AB, BC and CA repectively. Which one of the following relations is correct?

View Solution
