The log - log graph between the energy $E$ of an electron and its de - Broglie wavelength $λ$ will be

A

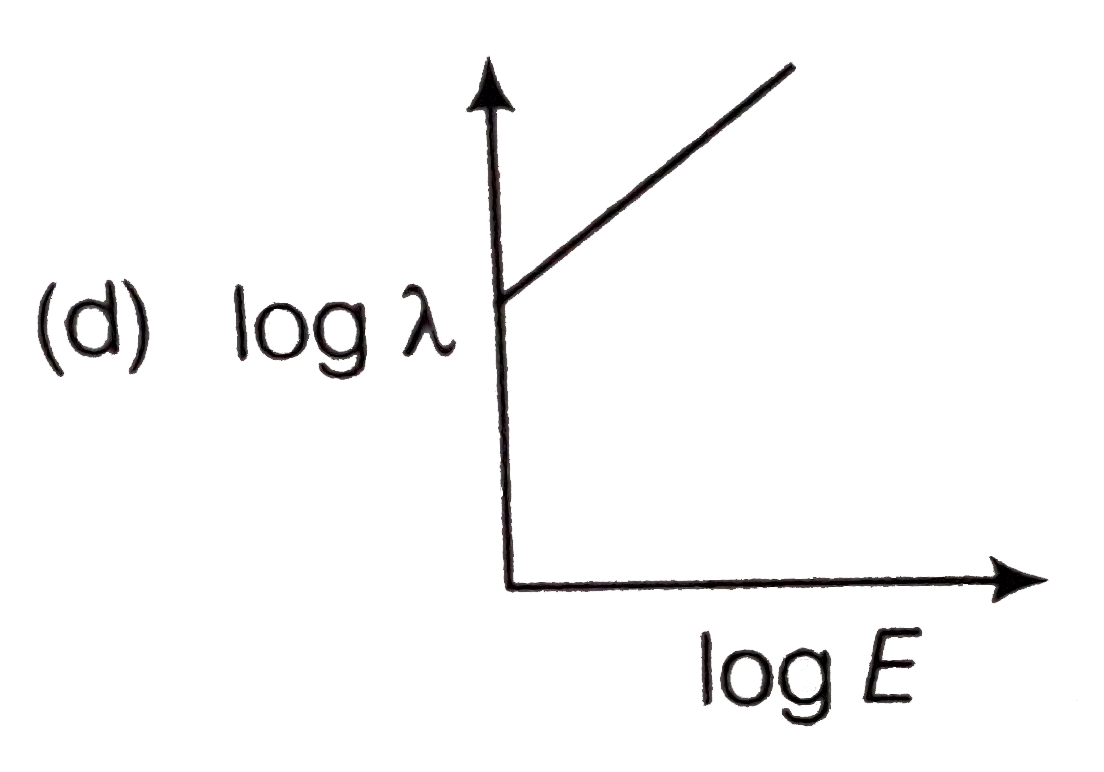
ocr_image

B

ocr_image

C

ocr_image

D

ocr_image

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

As we know that, wavelength of a particle
$λ = \frac{h}{\sqrt{2 m E}} = \frac{h}{\sqrt{2 m}} \frac{.1}{\sqrt{E}} \Rightarrow log λ = log (\frac{h}{\sqrt{2 m}} \frac{.1}{\sqrt{E}})$
$\Rightarrow log λ = \frac{log h}{\sqrt{2 m}} + \frac{log 1}{E^{1 / 2}}$
$\Rightarrow log λ = log (\frac{h}{\sqrt{2 m}}) - \frac{1}{2} log E$
$\Rightarrow log λ = - \frac{1}{2} log E + \frac{log h}{\sqrt{2 m}}$
So, equation of straight line is y=mx +c
This is equation of line with slope $- \frac{1}{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
de-Broglie wavelength $λ$ is
Aproportional to mass
Bproportional to impulse
Cinversely proportional to impulse
Dindependent to impulse
Question 2 - Select One
The de Broglie wavelength $λ$ of a particle
Ais proportional to mass
Bis proportional to impluse
Cis inversely proportional to impulse
Ddoes not depend on impulse
Question 3 - Select One
The de Broglie wavelength $λ$ of a particle
Ais proportional to mass
Bis proportional to impluse
Cis inversely proportional to impulse
Ddoes not depend on impulse

DC PANDEY-SOLVED PAPERS 2018-AIIMS

Home
Ask Doubt
Profile