Let C1,C2,,Cn be a sequence of concentric circle. The nth circle has the radius n and it has n openings. A points P starts travelling on the smallest circle C1 and leaves it at an opening along the normal at the point of opening to reach the next circle C2 . Then it moves on the second circle C2 and leaves it likewise to reach the third circle C3 and so on. Find the total number of different path in which the point can come out of nth circle.
Step by step video & image solution for Let C_1, C_2, ,C_n be a sequence of concentric circle. The nth circle has the radius n and it has n openings. A points P starts travelling on the smallest circle C_1 and leaves it at an opening along the normal at the point of opening to reach the next circle C_2 . Then it moves on the second circle C_2 and leaves it likewise to reach the third circle C_3 and so on. Find the total number of different path in which the point can come out of nth circle. by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
If C1,C2,C3,... is a sequence of circles such that Cn+1 is the director circle of Cn. If the radius of C1 is 'a', then the area bounded by the circles Cn and Cn+1, is
A2nπa2B22n−nπa2C2n−1πa2Dnone of theseTwo circles of radius 1 cm touch at point P. A third circle is drawn through the points A, B and C such that PA is the diameter of the first circle and BC perpendicular to AP is the diameter of the second circle. The radius of the third circle in cm.
A95B53C√102D2If the area of a circle is A, radius of the circle is r and circumference of it is C, then
AAr=CBrC=2ACCA=r2DAC=r24
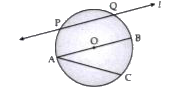
Take two points A and C on the circle, them the line segment joining the point A and C is called a ………... of the circle.
View SolutionConsider circles C1&C2 touching both the axes and passing through (4,4) , then the product of radii of these circles is
View SolutionA particle from the point P(√3,1) moves on the circle x2+y2=4 and after covering a quarter of the circle leaves it tangentially. The equation of a line along with the point moves after leaving the circle is
View Solution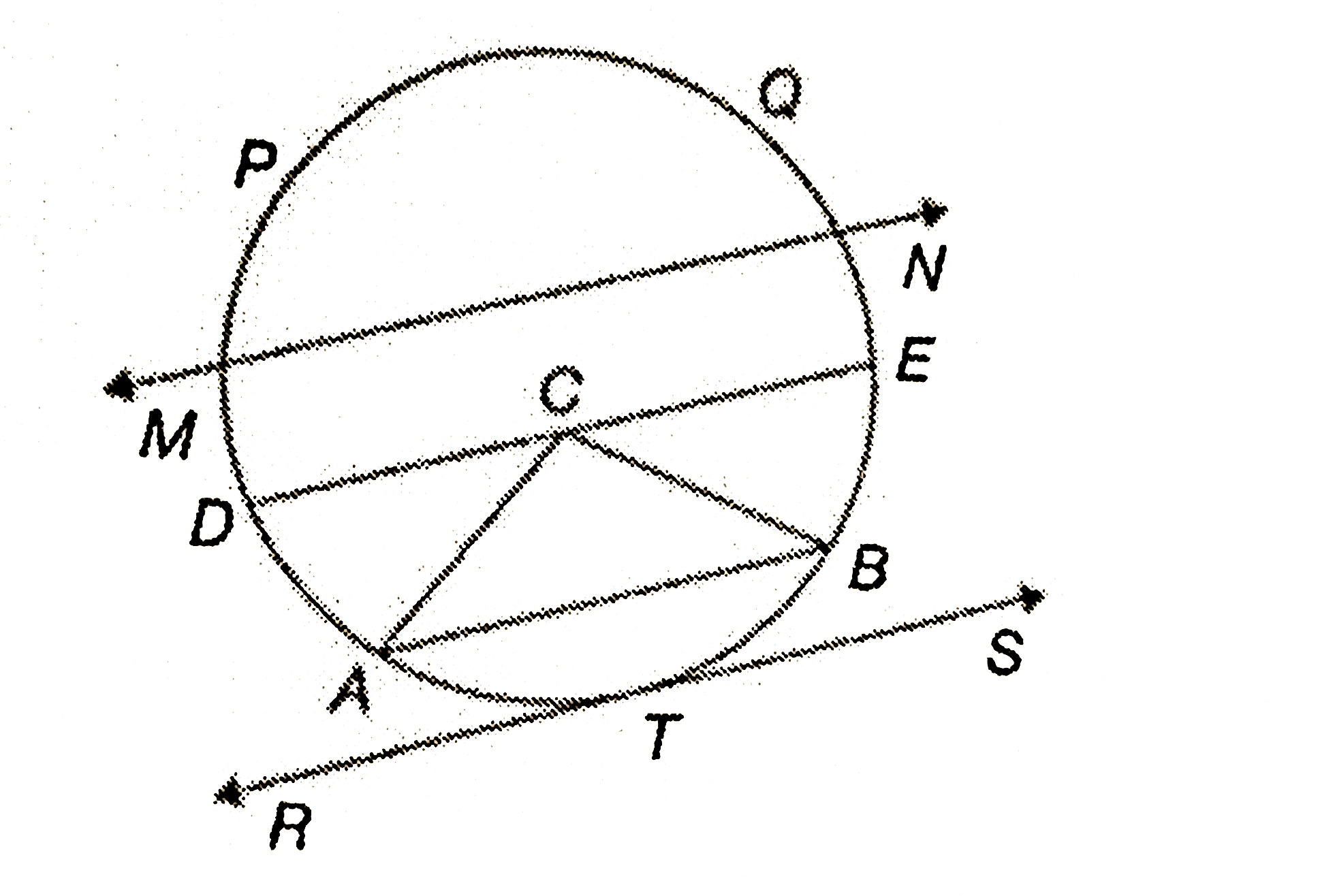
If 'C' is the centre of the circle and A is the point on the circle, then AC is called _______ of the circle.
View SolutionA circle x2+y2+4x−2√2y+c=0 is the director circle of circle S1andS2, is the director circle of circle S1, and so on. If the sum of radii of all these circles is 2, then find the value of c.
View Solution