is the formula of:
Laspeyre's Method
Paasche's Method
Fisher's Method
none of these
The correct Answer is:A
Topper's Solved these Questions
- INDEX NUMBERSBOOK - TARUN JAIN & VK OHRICHAPTER - INDEX NUMBERSEXERCISE - B. Choose appropriate word and fill in the blank
7 Videos
- INDEX NUMBERSBOOK - TARUN JAIN & VK OHRICHAPTER - INDEX NUMBERSEXERCISE - C. State whether the following statements are True or False
3 Videos
- INDEX NUMBERSBOOK - TARUN JAIN & VK OHRICHAPTER - INDEX NUMBERSEXERCISE - NCERT Questions (With Hints to Answers)
12 Videos
- FREQUENCY DIAGRAMS - HISTOGRAM, POLYGON AND OGIVEBOOK - TARUN JAIN & VK OHRICHAPTER - FREQUENCY DIAGRAMS - HISTOGRAM, POLYGON AND OGIVEEXERCISE - EXERCISE NCERT
7 Videos
- MEASURES OF CENTRAL TENDENCY - ARITHMETIC MEANBOOK - TARUN JAIN & VK OHRICHAPTER - MEASURES OF CENTRAL TENDENCY - ARITHMETIC MEANEXERCISE - Illustration
72 Videos
Similar Questions
Given the following table, find the Cost of living Index Number using Aggregate Expenditure Method bycompleting the activity.
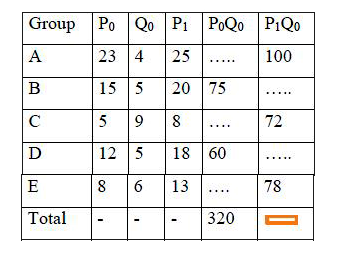
Therefore Cost of Living Index using Aggregate Expenditure method is
CLI =∑p1q0∑p0q0×100
=□
View SolutionSolve the following questions on the basis of the following questions on the basis of following functions
(a) P(n+1)=P(n)−P(n−1),P is the term of the sequence and P(0)=0,P(1)=1
(b) Q(n+1)=Q(n)+Q(n+1),Q is the term of the sequence and Q(0)=0,Q(1)=1
Which of the following can be a positive value of Qn+P(n+1)?
View Solution
Knowledge Check
The formula p01=∑p1q0∑p0q0×100 is for
ALaspeyre’s Price Index NumberBPaasche’s Price Index NumberCFisher’s Price Index NumberDWalsh’s Price Index Number∑p1q1w∑p0q0w×100 gives
AValue Index Number by Simple Aggregate methodBValue Index Number by Weighted Aggregate methodCCost of Living Index NumberDLaspeyre’s Index NumberSolve the following questions on the basis of the following questions on the basis of following functions
(a) P(n+1)=P(n)−P(n−1),P is the term of the sequence and P(0)=0,P(1)=1
(b) Q(n+1)=Q(n)+Q(n+1),Q is the term of the sequence and Q(0)=0,Q(1)=1
The value of Q(n−1)+Q(n+1)+L(n−1)+L(n+1) cannot be :A30B75C18D122
Solve the following questions on the basis of the following questions on the basis of following functions
(a) P(n+1)=P(n)−P(n−1),P is the term of the sequence and P(0)=0,P(1)=1
(b) Q(n+1)=Q(n)+Q(n+1),Q is the term of the sequence and Q(0)=0,Q(1)=1
The value of Q[Q(n+1)] can be :
View SolutionSolve the following questions on the basis of the following questions on the basis of following functions
(a) P(n+1)=P(n)−P(n−1),P is the term of the sequence and P(0)=0,P(1)=1
(b) Q(n+1)=Q(n)+Q(n+1),Q is the term of the sequence and Q(0)=0,Q(1)=1
The value of Qn+Pn cannot be :
View SolutionSolve the following questions on the basis of the following questions on the basis of following functions
(a) P(n+1)=P(n)−P(n−1),P is the term of the sequence and P(0)=0,P(1)=1
(b) Q(n+1)=Q(n)+Q(n+1),Q is the term of the sequence and Q(0)=0,Q(1)=1
The vlaue of [Q(n)]pn can be :
View SolutionSolve the following questions on the basis of the following questions on the basis of following functions
(a) P(n+1)=P(n)−P(n−1),P is the term of the sequence and P(0)=0,P(1)=1
(b) Q(n+1)=Q(n)+Q(n+1),Q is the term of the sequence and Q(0)=0,Q(1)=1
The value of Qn×Pn can be :
View SolutionSolve the following questions on the basis of the following questions on the basis of following functions
(a) P(n+1)=P(n)−P(n−1),P is the term of the sequence and P(0)=0,P(1)=1
(b) Q(n+1)=Q(n)+Q(n+1),Q is the term of the sequence and Q(0)=0,Q(1)=1
The value of P cannot be :
View Solution
