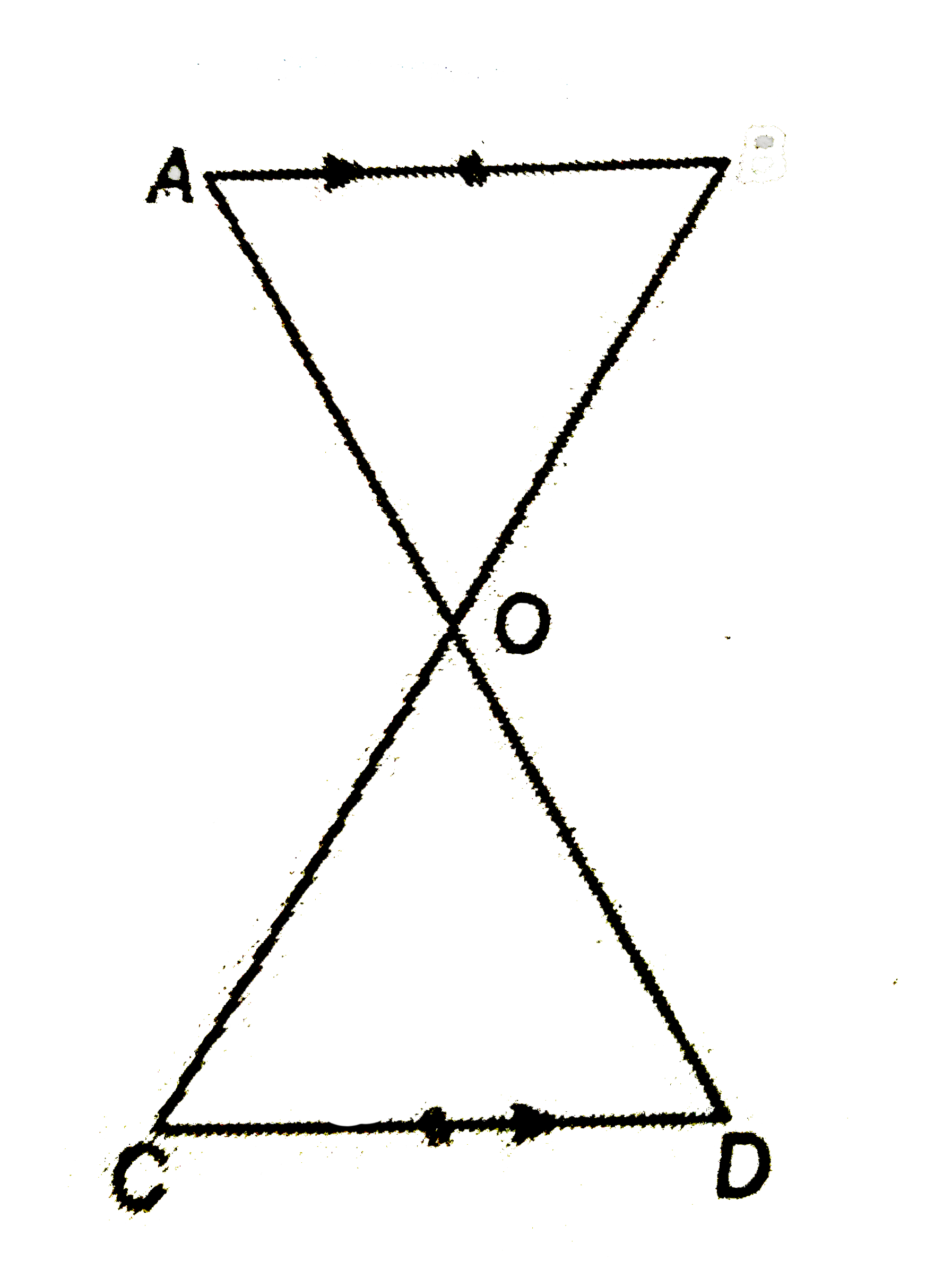
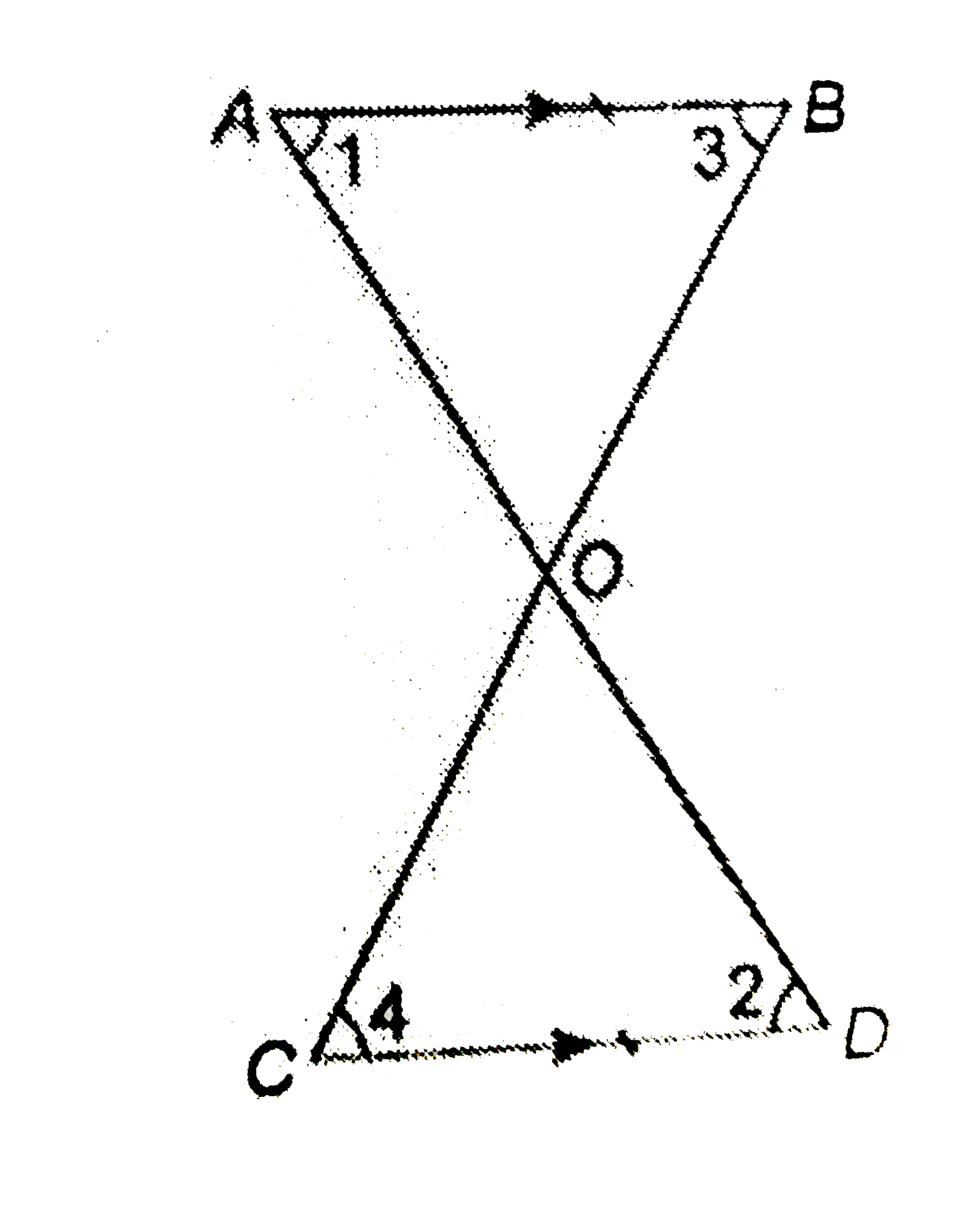
In the adjoining figure, AB = CD and AB||CD prove that
(i)
(ii) AD and BC bisect each other at the point O.
Video Solution
Text Solution
(i) since AB||CD (given)
and (alternate angles)
Now, in and ,
Therefore, (ASA) Hence Proved.
(ii) Therefore, (c.p.c.t.)
bisects AD.
Also (c.p.c.t)
bisects BC.
Hence, AD and BC bisect each other. Hence Proved.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar5videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7a35videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)10videos
SURFACE AREA AND VOLUME
Similar Questions
Knowledge Check
- Question 1 - Select One
In the adjoining figure AB∣∣CDandPQ=SR, then :
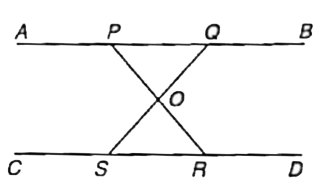 APQ=PSBSR=RPCPS=QRDAP=RD
APQ=PSBSR=RPCPS=QRDAP=RD - Question 2 - Select One
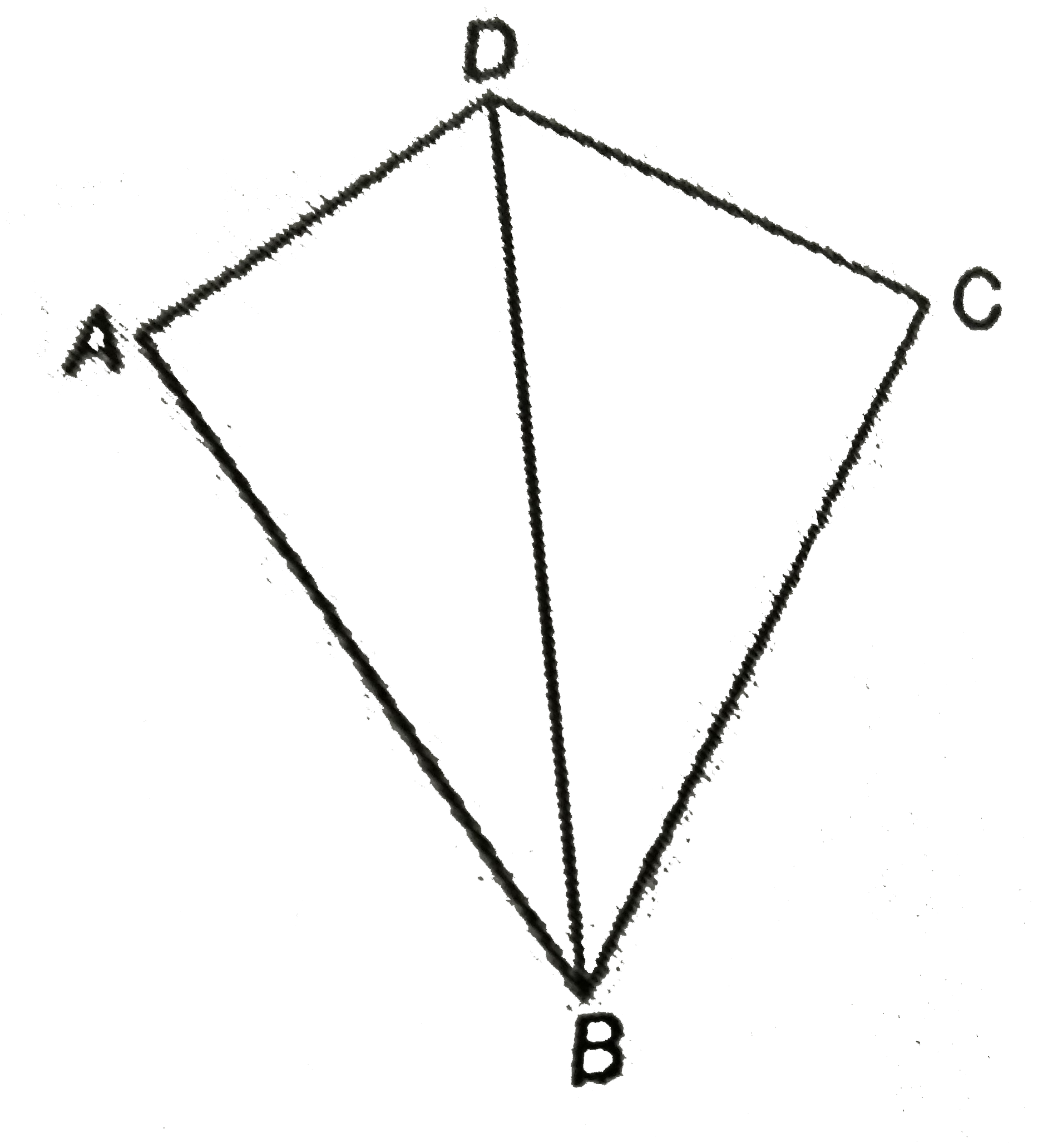
In the adjoining figure, if AB = AD and CB = CD, then whch of the following is correct?
 AΔABC≅ΔADCB∠BCA=∠DCAC∠ADC=∠ABCDAll of these
AΔABC≅ΔADCB∠BCA=∠DCAC∠ADC=∠ABCDAll of these
In the adjoining figure AB||CD, find x and y
 View Solution
View SolutionIn Figure, if AB=AC and BE=CD, prove that AD=AE.
 View Solution
View SolutionIn the given figure, AB = CD and AD = CB. Prove that ΔABD≅ΔCDB.
 View Solution
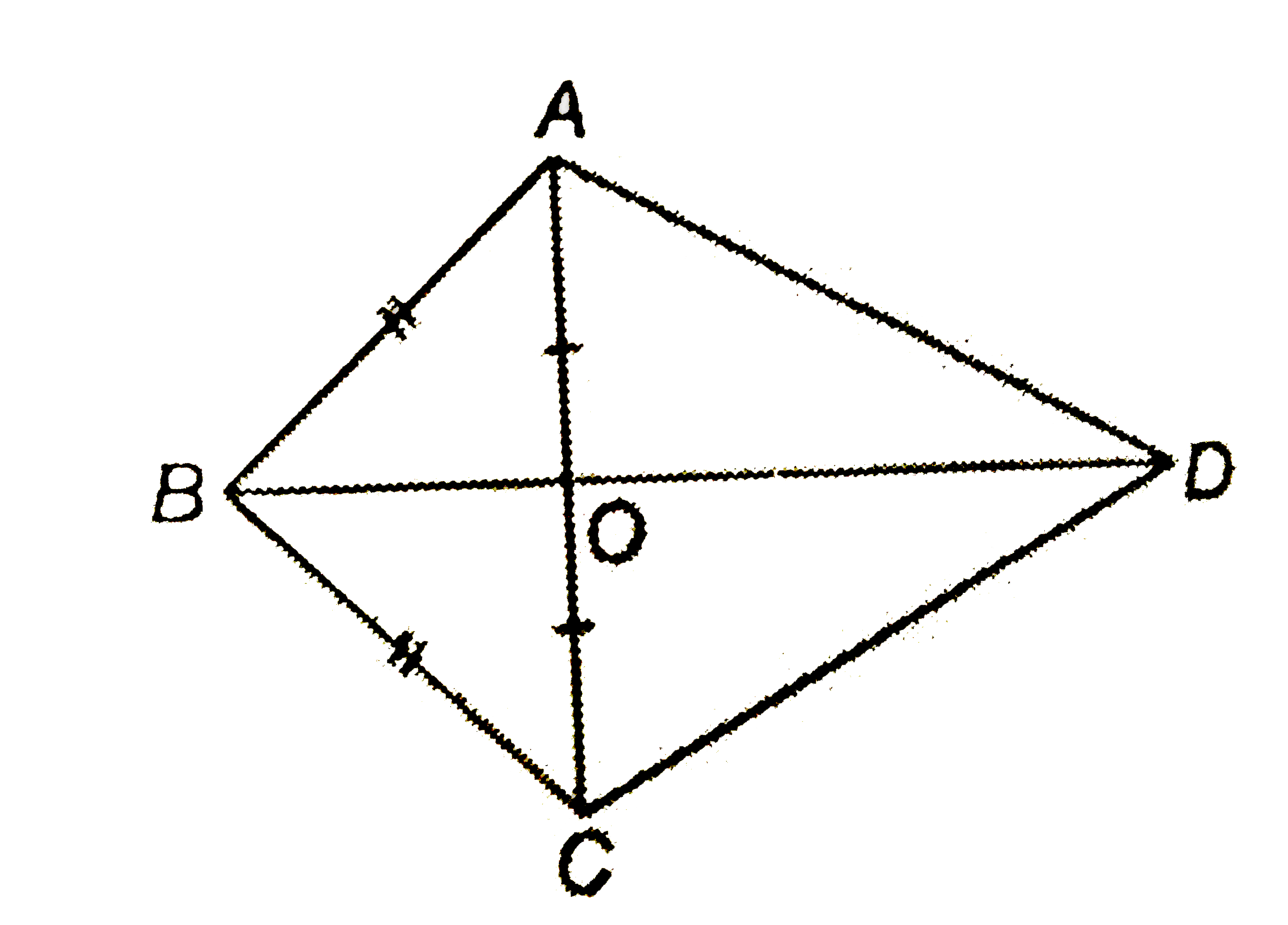
View SolutionIn the following figure, OA = OC and AB = BC. Prove that :
(i) ∠APB=90∘
(ii) ΔAOD≅ΔCOD
(iii) AD=CD
 View Solution
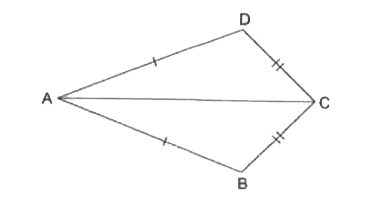
View SolutionIn the adjoining figure,
AB = AD and CB = CD.
Is △ABC≅△ADC ?,
 View Solution
View SolutionIn the figure it is given that AB=CD and AD=BC. Prove that ΔABC≅ΔCDA.
 View Solution
View Solution