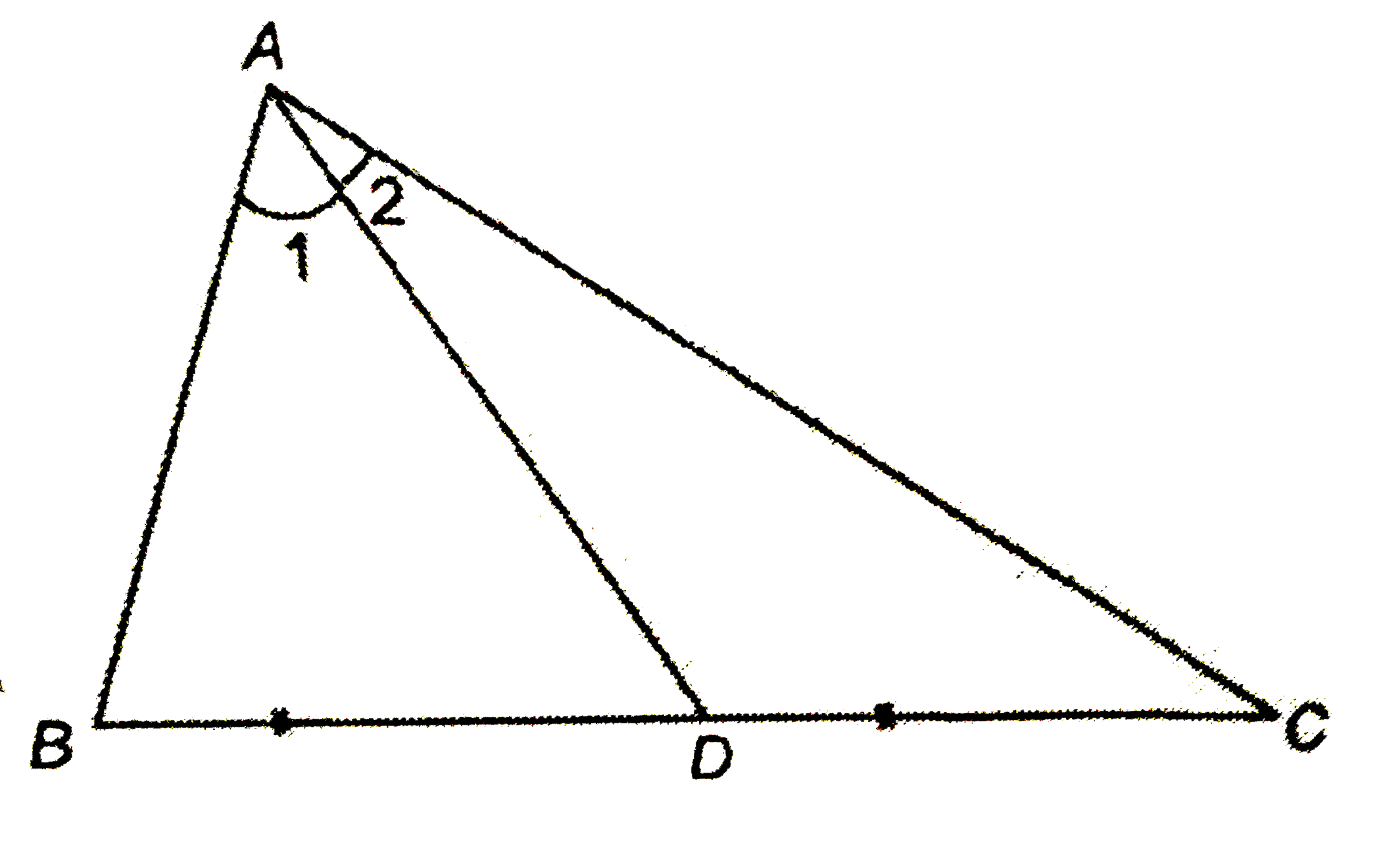
If the bisector of the vertical angle of a triangle bisects the base of the triangle. then the triangle is isosceles. GIVEN : A ABC in which AD is the bisector of ∠A meeting BC in D such that BD=DC. TO PROVE : ABC is an isosceles triangle.
It seems that for proving the triangles to be congruent, we have ∠1=∠2,AD=AD and BD=DC and so, triangles are congruent. But you see the ease of congruency. It is ASS , which is not the case of any congruency. So we will see this problem with a different view.
Construction : Produce AD to E such that AD=DE.
Proof : In ΔABD and ΔECD,
∵⎧⎪⎨⎪⎩BD=DC(Given as D is the mid-point)∠3=∠4(VOA)AD=DE(construction)
∴ΔABD≅ΔECD (SAS)
∴AB=EC (c.p.c.t) ...(1)
and ∠1=∠5 (c.p.c.t) ...(2)
But ∠1=∠2 (given) ...(3)
∴∠2=∠5 [fro (2) and (3)]
⇒ EC=AC ...(4)
( ∵ sides opposite to equal angles are equal)
∴ from (1) and (4), we have
AB=AC
∴ΔABC is an Isosceles triangle. Hence Proved.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar5videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7a35videos
TRIANGLES
- BOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)10videos
SURFACE AREA AND VOLUME
Similar Questions
If the bisector of the vertical angle of a triangle bisects the base, prove that the triangle is isosceles.
View SolutionJoinA→D
Hence,AD∥BC
∠ACB=∠CAD(alternateangle
∠BAC=∠ACD(alternateangle)
HenceAB=AC (by ASA congurency )so, it is isosceles triangle.View SolutionIf the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
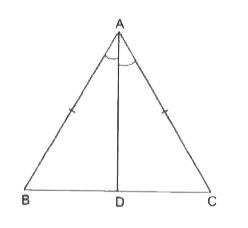
View SolutionProve that the bisector of the vertical angle of an isosceles triangle bisects the base at right angles.
 View Solution
View SolutionShow that the bisector of vertical angle of an isosceles triangle bisects the base at right angles.
View SolutionIf the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
View SolutionIf the altitude from one vertex of a triangle bisects the opposite side, then the triangle is isosceles. GIVEN : A ABC such that the altitude AD from A on the opposite side BC bisects BC i.e., BD=DC. TO PROVE : AB=AC i.e. the triangle ABC is isosceles.
View SolutionProve that median from the vertex of an isosceles Triangle is the bisector of the vertical angle
View SolutionThe bisectors of the angles B and C of a triangle ABC , meet the opposite sides in D and E respectively. If DE||BC , prove that the triangle is isosceles.
View SolutionIf one angle of a triangle is equal to the sum of the other two angles, then the triangle is an isosceles triangle (b) an obtuse triangle an equilateral triangle (d) a right triangle
View Solution

