Show that the difference of any two sides in a triangle is smaller than the third side.
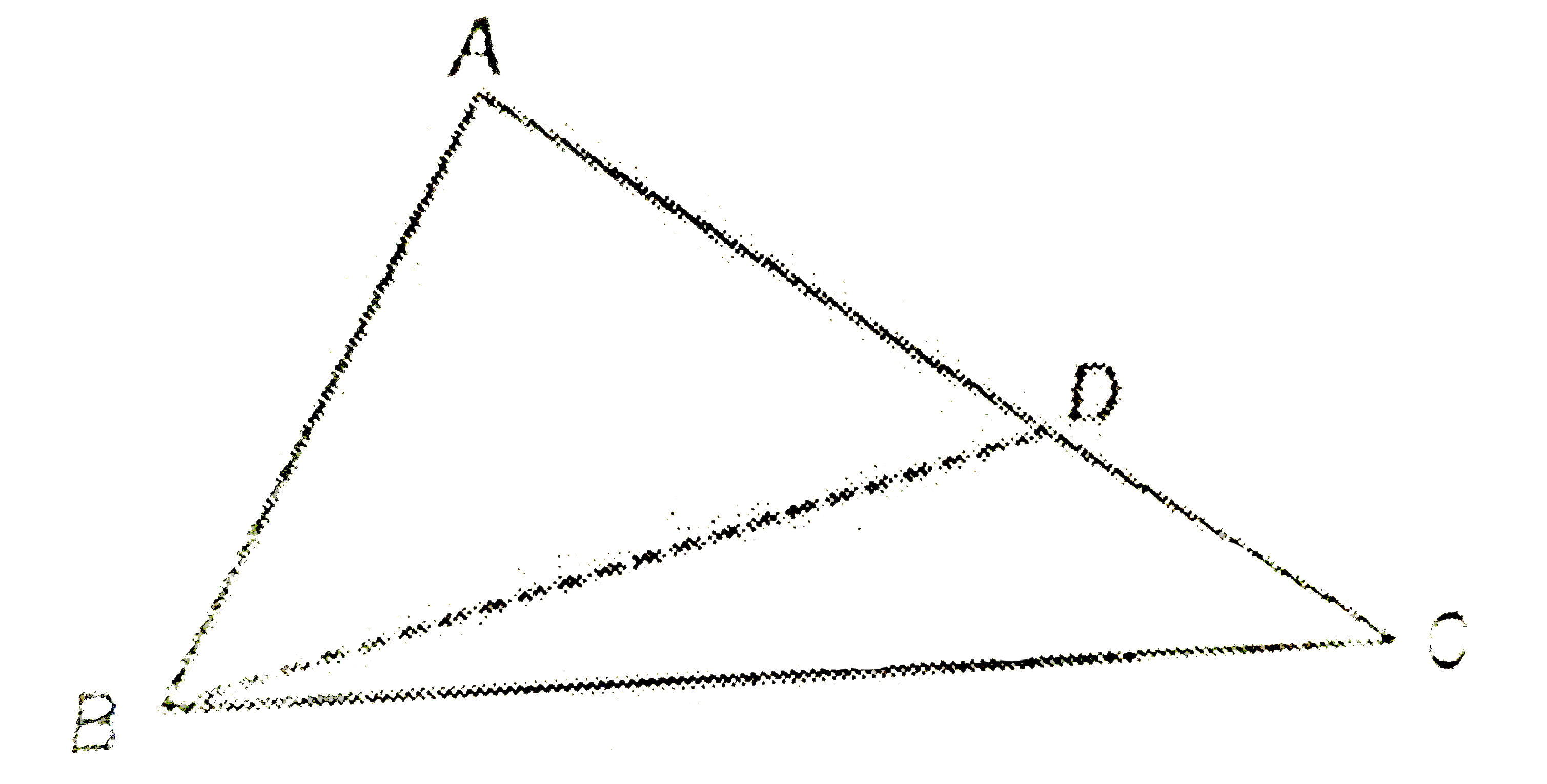
Given : ΔABC in which AC>AB.
To prove : AC−AB<BC
Construction : Cut AB = AD from AC. Join BD. ltbr> Proof : ∠BDC is the exterior angle of ΔABD.
∴∠BDC−∠ABD+∠BAD.
( ∵ the exterior angle is equal t the sum of opposite interior angles of a triangle.)
⇒ ∠BDC>∠ABD ...(1)
Again ∠ADB is the exterior angle of ΔDBC
∴∠ADB=∠DBC+∠BCD
⇒ ∠ADB>∠DBC
but AB=AD
∴∠ABD=∠ADB
Therefore n=∠ABD>∠DBC ...(2)
From (1) and (2), we have
∠BDC<∠DBC
⇒ BC>DC (∵ side opposite to larger angle is larger)
⇒ DC<BC
⇒ AC−AD<BC
⇒ AC−AB<BC (∵AD=AB)
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7a
35 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
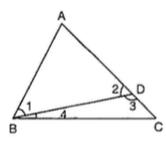
Show that the difference of any two sides of a triangle is less than the third side. Given : A ABC To Prove: (i) AC−AB<BC BC−AC<AB (iii) BC−AB<AC Construction: Take point D on AC such that AD=AB . Join BD
View SolutionShow that the difference of any two sides of a triangle is less than the third side. GIVEN : ABC TO PROVE : (i) AC−AB<BC BC−AC<AB (iii) BC−AB<AC CONSTRUCTION : Take a point D on AC such that AD=AB. Join BD.
View SolutionThe difference of any two sides of a triangle is _______ than the third side .
View SolutionSum of any two sides of a triangle is greater than the third side.
View SolutionSum of any two sides of a triangle is not less than the third side
View SolutionThe sum of any two sides of a triangle is greater than third side.
View SolutionThe difference between the lengths of any two sides of a triangle is smaller than the length of third side.
View SolutionFill in the blanks to make the following statements true: In a right triangle the hypotenuse is the ...... side. The sum of three altitudes of a triangle is ......... than its perimeter. The sum of any two sides of a triangle is ......... than the third side. If two angles of a triangle are unequal, then the smaller angle has the ........... side opposite to it. Difference of any two sides of a triangle is ......... than the third side. If two sides of a triangle are unequal, then the larger side has ..... angle opposite to it.
View SolutionProperty The sum of any two sides of a triangle is greater than the third side.
View SolutionThe sum of any two sides of a triangle is _______ than the third side .
View Solution
