An equilateral triangle if its altitude is 3.2cm.
Text Solution
Steps of construction :
1. Draw a line l.
Mark any point D on the line l.
3. At point D, draw →DX⊥l and cut DA=3.2cm from →DX.
4. At the point A, construct AB and AC which meets the l at points B and C respectively such that
∠=30∘ and ∠DAC=30∘
Then, ΔABC is the required equilateral triangle
because ∠ABC=180∘−(90∘+30∘)=60∘.
∠ACB=180∘−(90∘+30∘)=60∘.
and ∠BAC=30∘+30∘=60∘
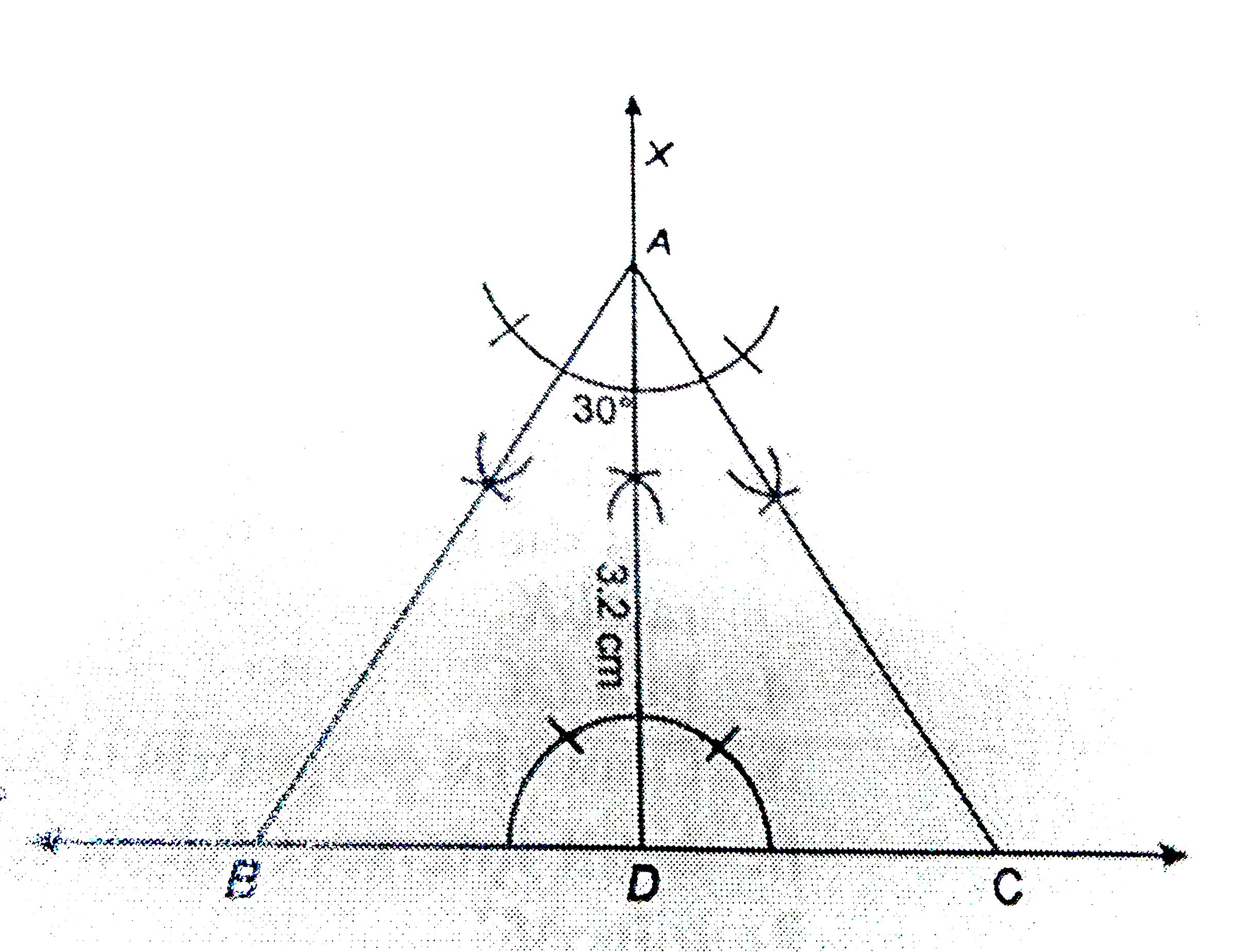
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the altitude of an equilateral triangle of side 8 cm.
A5√3B3√3C4√3D2√3If each side of an equilateral triangle is 12 cm, then its altitude is equal to:
A6√2cmB3√2 cmC6√3cmD3√6 cmFind the length of the altitude of an equilateral triangle of side 9√3cm.
A21 cmB15.5 cmC14 cmD13.5 cm
Each side of an equilateral triangle is 6 cm. Its altitude is
View SolutionFind the area of an equilateral triangle having altitude h cm.
View SolutionFind the altitude of an equilateral triangle of side 8 cm.
View SolutionThe length of an altitude in an equilateral triangle of side 'o' cm is ……………. .
View SolutionThe altitude of an equilateral triangle of side 2√3 cm is -----
View Solution
