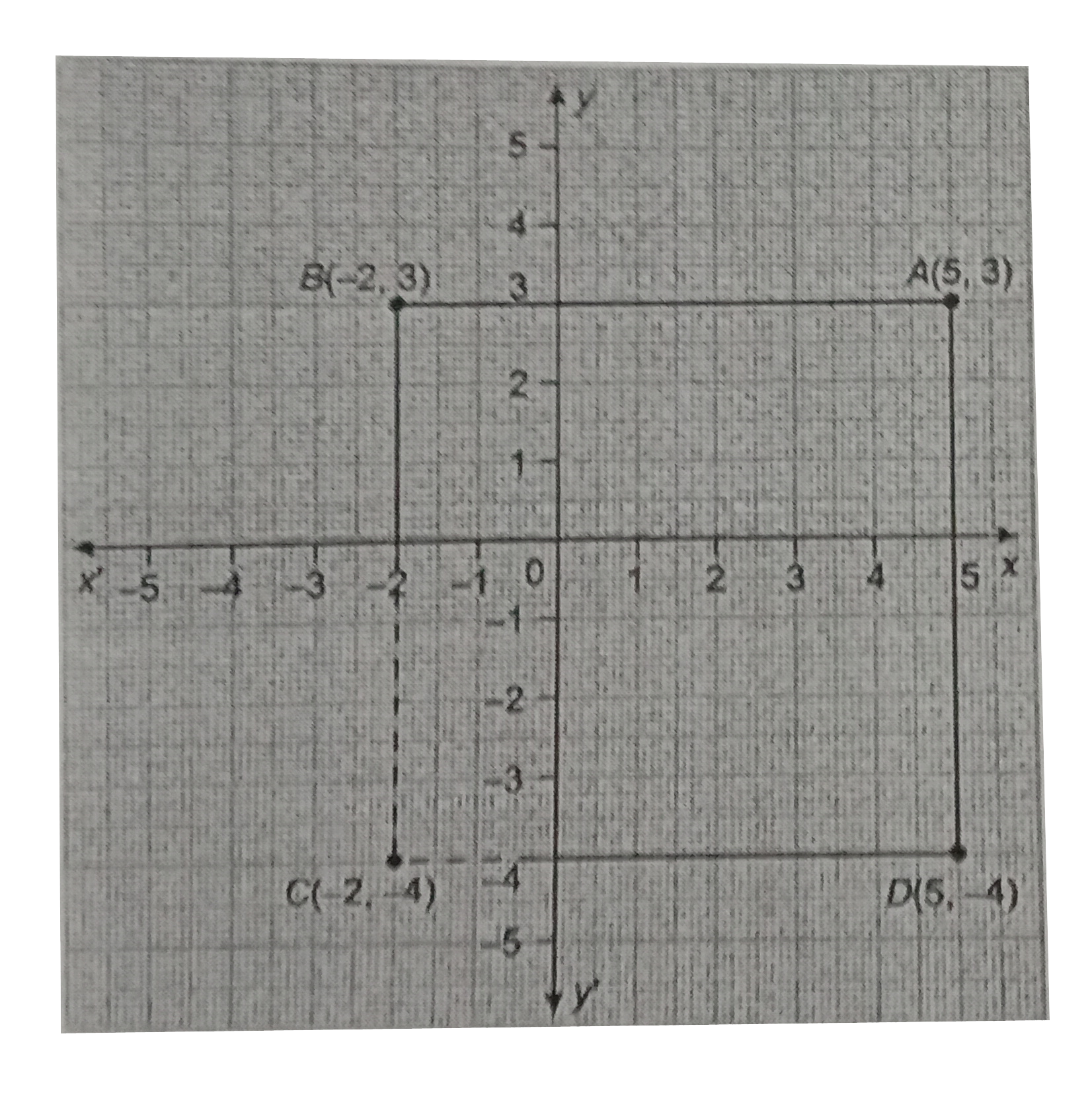
Points A(5,3),B(−2,3) and D(5,−4) are three vertices of a square ABCD. Plot these points on a graph paper and hence, find the coordinate of the vertex C.
Plot the points A(5,-3),B(-2,3) and D(5,-4). Join AB and AD. Since ABCD is a square, so all the sides are equal and each is of 90∘meaure. Therefore, the absissa of the vertex C will be −2 and ordinate −4. Hence, the co-ordinates of the vertex C are (−2,−4) .
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Revision Exercise8videos
CO-ORDINATE GEOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise8videos
CO-ORDINATE GEOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise8videos
CO-ORDINATE GEOMETRY
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Revision Exercise (long Answer Questions )5videos
CIRCLE
- BOOK - NAGEEN PRAKASHANCHAPTER - CONSTRUCTIONSEXERCISE - EXAMPLE SOLUTION.19videos
CONSTRUCTIONS
Similar Questions
A(3,6),B(3,2) and C(8,2) are the vertices of a rectangle. Plot these points on a graph paper and then use it to find the co-ordinates of vertex D.
View SolutionA(−2,2),B(8,2) and C(4,−4) are the vertice of a parallelogram ABCD. By plotting the given points on a graph paper, find the co-ordinates of the fourth vertex D.
View Solution
Knowledge Check
- Question 1 - Select One
The points A(4,5,10),B(2,3,4)andC(1,2,−1) are three vertices of a parallelogram ABCD, then
AVector equation of AB is 2i+3j+4k+λ(i+j+3k)BCartesian equation of BC is x−21=y−31=z−4−5CCoordinate of D are (3,4,5)DABCD is a rectangle. - Question 2 - Select One
If A (1,3),B(-1,2),C(2,5) and D(x,4) the vertices of □ABCD
them find the value of x .A0B5C6D7
Plot the following points on a graph paper:
(3,2)View SolutionPlot the following points on a graph paper:
(2,2)View SolutionThree vertices of a rectangle are (3,2),(4,2). and (−4,5). Plot these points and find the coordinates of the fourth vertex.
View SolutionShow that the points A(0, 6), B(2, 1) and C(7, 3) are three corners of a square ABCD. Find (i) the slope of the diagonal BD and (i) the coordinates of the fourth vertex D.
View SolutionThe three vertices of a square ABCD are A(3,2),B(−2,2)andD(−3,3). Plot these points on a graph paper and hence, find the coordinates of C. Also, find the area of square ABCD.
View SolutionShow that the points A(3,5),B(6,0)mC(1,−3)andD(−2,2) are the vertices of a square ABCD.
View Solution

