Find the area of the region bounded by the curve y2=xand the lines x=1,x=4and the x-axis.
Video Solution
Text Solution
y2=x is a symmetric curve about X-axis. ABCDA is the region bounded by x=1,x=4 and y2=x and X-axis.
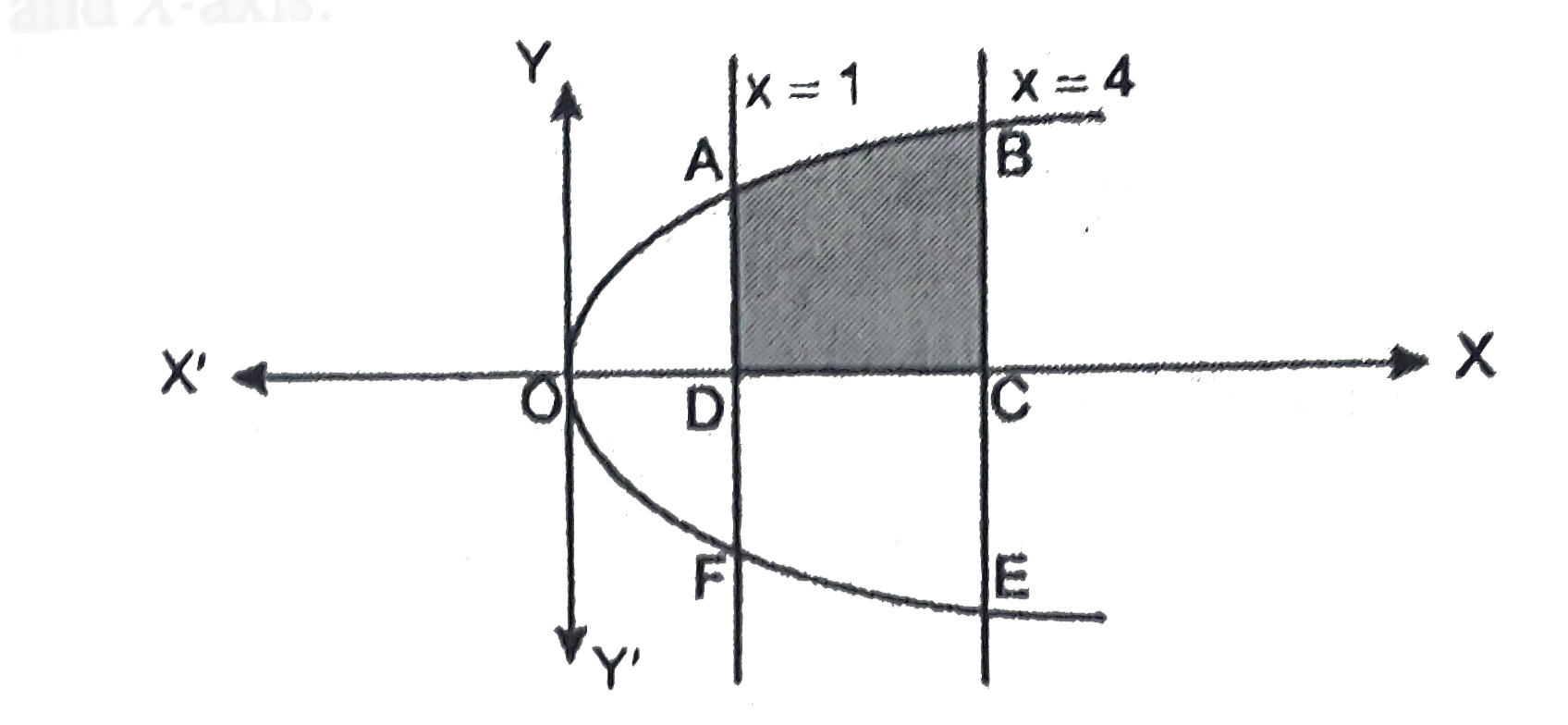
Required area = area of ABCDA
=∫41|y|dx=∫41√xdx
=[x3/23/2]41=23[43/2−13/2]
=23(8−1)=143 sq. units.
|
Topper's Solved these Questions
- APPLICATIONS OF INTEGRALSBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF INTEGRALSExercise:Exercise 8.2
Explore 7 Videos
- APPLICATIONS OF INTEGRALSBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF INTEGRALSExercise:Miscellaneous Exercise
Explore 19 Videos
- APPLICATIONS OF INTEGRALSBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF INTEGRALSExercise:Exercise 8 C Questions For Competitive Examinations
Explore 10 Videos
- APPLICATIONS OF DERIVATIVESBook:NAGEEN PRAKASHANChapter:APPLICATIONS OF DERIVATIVESExercise:Miscellaneous Exercise
Explore 24 Videos
- Continuity and DifferentiabilityBook:NAGEEN PRAKASHANChapter:Continuity and DifferentiabilityExercise:Miscellaneous Exercise
Explore 23 Videos
Similar Questions
Knowledge Check
The area of the region bounded by the curve y=x2 and the line y=16 is :
A323B2563C643D1283The area bounded by the curve y2=14x and the lines x = 1, x = 4 above X-axis is
A73sq.unitsB143sq.unitsC283sq.unitsD563sq.unitsThe area of the region bounded by the curves y = | x – 2 l, x = 1, x = 3 and the x-axis is
A3B2C1D4
Find the area of the region bounded by the curve y=x2 and the line y=4.
View SolutionFind the area of the region bounded by the curve xy=1 and the lines y=x,y=0,x=e
View SolutionFind the area of the region bounded by the curve y=x2 and the line y=4.
View SolutionFind the area of the region bounded by the curve (y−1)2=4(x+1) and the line y= x-1
View SolutionFind the area of the region bounded by the curve y2=4x and x2=4y.
View Solution