Explain the working of Carnot's heat engine with the help of graph.

Text Solution

Verified by Experts

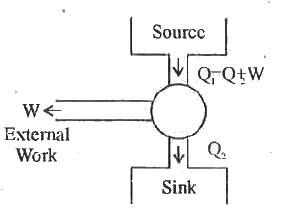
Working of Carnot.s engine :
Step 1 : The working substance (ideal gas) is enclosed in a non-conducting wall and conducting bottom of a cylinder fitted with air tight non conducting piston. This is placed on the source having an infinite thermal capacity at a steady temperature. The top surface is conducting and the rest non conducting. As a result, the gas expands isothermally. The work done by the system,
$W_{1} = μ R T_{1} log \frac{V_{2}}{V_{1}}$ (Curve A B)
Step 2 : The working substance is now placed on a non conducting platform, as a result of which no heat exchange takes place between the system and the surroundings. The system expands adiabatically at the expense of its internal energye. The gas cools. The work done by the system,
$W_{2} = \frac{μ R}{γ - 1} (T_{1} - T_{2})$ (Curve B C)

Step 3 : The working substance is now placed on the sink maintained at a steady low temperature $T_{2} K$ . The symstem undergoes isothermal compression at this temperature. The pressure of gas increases and volume decreases without any chagne in the internal energy and specific heat of gas remains at infinity.
$W_{3} = μ R T_{2} log (\frac{V_{4}}{V_{3}})$ (Curve C A)
Step 4 : The working substance is placed on a non-conducting platform. Under thermal isolation, the system undergoes Extermal change in its intcrnal energy and its specific heat remains at Work zero. Adiabatic compression results in increase in the presssure and temperature at the expense of work being done on the
For $η_{1} = η_{2}, \frac{T_{1}}{T_{2}} = \frac{T_{1}^{1}}{T_{2}^{1}} and \frac{Q_{1}}{Q_{2}} = \frac{Q_{1}^{1}}{Q_{2}^{1}}$ .
For refrigerators (reverse Carnot.s engine)
coefficient of performance $β = \frac{Q_{2}}{W} = \frac{Q_{2}}{Q_{1} - Q_{2}}$
W- Work done on the system.
$Q_{2}$ - Heat extracted from the cold reservoir
$Q_{1}$ - Heat rejected to the surrounding.
Coefficient of linear expansion $α = \frac{(change in length)}{(original length)(rise in temperature)}$
i.e., $α = \frac{(l_{2} - l_{2})}{l_{1} (θ_{2} - θ_{1})} K^{- 1}$
Coefficient of superficial expansion $β = 2 α = \frac{Δ A}{A (θ_{2} - θ_{1})} K^{- 1}$
Coefficient of volume expansion $γ = 3 α = \frac{Δ V}{V (θ_{2} - θ_{1})} K^{- 1}$
First Law of Thermodynamies, $d Q = d U + d W$ .
$Q = m s θ, where s = \frac{Q}{m θ} J k g^{- 1} K^{-}$
Thermal capacity of a substance $= (m s) J K^{- 1}$
$C_{P} - C_{V} = R and C_{P} - C_{V} = r$
$d S = \frac{d Q}{T}$ where dS = change in entropy
T= steady transition temperature.
Classius - Clapeyron equation,
$\frac{d P}{d T} = \frac{L}{T (V_{2} - V_{1})}$ where L- latent heat rate of change of pressure with temperature per kg of substance.
For $V_{2} > V_{1}$ as in the transition of liquid state to gasesous state, implies that increase of pressure increases the boiling point of liquids.
For $V_{2} < V_{1}$ as in the case of melting of ice (water like substances)
$V_{2} - V_{1} - v e and (\frac{d P}{d T})$ is negative.
This implies increase of pressure decreases the freezing point of liquide below $0^{\circ} C$ . For $V_{2} - V_{1} = + v e$ (wax like substances), increase of pressure increases the melting poin of solids.
Expressions for adiabatic processes:
$P_{1} V_{1}^{γ} = P_{2} V_{2}^{γ}$
$T_{1} V_{1}^{γ - 1} = T_{2} V_{2}^{γ - 1}$ .
$T_{1} P_{1} \frac{1 - γ}{γ} = T_{2} V_{2} \frac{1 - γ}{γ} or T = K P \frac{γ - 1}{γ}$
Vander Waal equation for real gases:
$(P + \frac{μ^{2} a}{V^{2}}) (V - μ b) = μ R T$
where $μ$ = number of moles
V= volume of the container
$μ b$ = volume of $μ$ moles of gas
$\frac{μ^{2} a}{V^{2}}$ = pressure due to intermolecular collisions.
Coefficient of performance of Carnot refrigerator,
$β = \frac{Q_{2}}{Q_{1} - Q_{2}} = \frac{Q_{2}}{W} = \frac{Heat extracted from cold reservoir}{Work done by compressor motor}$

Updated on:21/07/2023

The efficiency of a Carnot heat engine
Ais independent of the temperature of the source and the sink
Bis independent of the working substance
Ccan be $10 %$
Din not affected by the thermal capacity of the source of the sink
Efficiency of a Carnot heat engine may be given as
A $\frac{w}{Q_{2}}$
B $1 - \frac{Q_{2}}{Q_{1}}$
C $1 - \frac{T_{1}}{T_{2}}$
DNone of these
The temperature of the source of Carnot's heat engine is $T_{1}$ , and that of sink is $T_{2}$ having efficienty 0.5. The efficiency of another Carnot's heat engine is also 0.5. The temperature of source and sink of the second engine are respectively.
A $2 T_{1}, 2 T_{2}$
B $2 T_{1}, \frac{T_{2}}{2}$
C $T_{1} + 5, T_{2} - 5$
D $T_{1} + 10, T_{2} - 10$