Question

Show that $n=\frac{\sin \left(\frac{A+D}{2}\right)}{\sin \left(\frac{A}{2}\right)}$ where symbols have their usual notations.

Explanation

BC - Base of the prism
AB and AC - Refracting sides representing the planes
ABC - Principle section of prism.
PQ - incident ray.
RS - emergent ray
`d_(1)` - angle of deviation `d_(1)=i_(1)-r_(1)`
`d_(2) ` - angle of deviation `d_(2)=i_(2)-r_(2)`
`u hatTS `- d - total angle of deviation or net deviation
i.e., `d=d_(1)+d_(2)` (exterior angle = sum of two opposite interior angles)

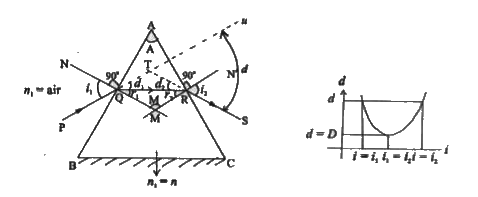
NM is normal to AB at Q
N.M is normal to AC at R
`i_(1)`- angle of incidence
`i_(2)` - angle of emergence.
D = angle of minimum deviation,
From figure (1)
From the quadrilateral AQMR,
`A hatQM~=A hatRM=90^(@)` (Nm, N.M are normal to AB and BC)
So that `A+M=180^(@)" "` ......(1)
`therefore `AQMR is a cyclic quadrilateral. From the triangle QMR
`r_(1)+r_(2)+hatM=180^(@) ("Property of a "Delta) " " `......(2)
From (1) and (2)
`A+M=r_(1)+r_(2)+M`
i.e., `A=r_(1)+r_(2)" "`.......(3)
For non-symmetric condition `i_(1) ne i`
`d_(1) ne d_(2)` also net deviation d.
`d=d_(1)+d_(2)`
`d=i_(1)-r_(1)+i_(2)-r_(2)`
`therefore d=i_(1)+I_(2)-(r_(1)+r_(2))`
using (3) we write,
`d=i_(1)+i_(2)-A" "`.......(4)
from the fig., we note that for non-symmetric condition for two angles of incidence, angle of net deviation is the same. However for a symmetric condition, `i_(1)=i_(2)=i and r_(1)=r_(2)=r` net deviation becomes the minimum angle of deviation. In this case the refracted ray will be parallel to the base.
`therefore` for symmetric condition,
(4) can be written as `D=2i-A`
i.e., `i=((A+D)/(2))" "` ......(5)
(3) can be written as,
`A=2r`
or `r=((A)/(2))" " ` ......(6)
From Snell.s law of refraction at AB,